Előszó

Ez itten egy F-15 vadászgép. Szép, szép, de mire képes? Mekkora a csúcssebessége? Mennyire jól gyorsul? Milyen gyorsan emelkedik? Milyen messzire repül el? Milyen gyorsan fordul? Megannyi kínzó kérdés. Na és ha a képen látható fegyverzetet hordozza, légiharcrakétákkal mi a helyzet? Na és mi van akkor, ha még ennél is több és nehezebb fegyvert hordoz? Lássuk hát, hogy mire képesek a vadászgépek helyzettől függően.

Ahhoz, hogy megértsük a vadászgépek teljesítményparamétereit szükséges tisztában lenni azzal, hogy milyen fő tényezők befolyásolják azt.

• Az egyik a repülőgép tömege, ami függ a hordozott függesztményektől és az aktuális üzemanyag-mennyiségtől. Minél nagyobb tömeget kell gyorsítani, annál nagyobb erő kell ahhoz egy adott gyorsulás eléréséhez.
• Másik fontos tényező a repülőgép légellenállása, a sárkányszerkezet légellenállásán túl ezt is befolyásolják a függesztmények.
• A hajtómű vagy hajtóművek tolóereje. A csatorna fókusza a sugárhajtású vadászgépeken van ezért mindig tolóerőről fogunk beszélni, a vonóerőt előállító légcsavaros gépekkel nem foglalkozunk.
• A repülési magasság és a külső hőmérséklet. A levegő sűrűség- és hőmérsékletének változásának nagyon komoly hatása van a tolóerő- és a felhajtóerőre is.
• 

Ez a négy tényező határozza meg a repülőgép maximális teljesítményét, illetve az üzemanyag fogyasztását adott sebességen és magasságon. Egy vadászgép csúcssebessége és üzemanyag fogyasztása nem egy állandó érték, ahogy bármilyen más járműé sem. Egészen más a gyorsulása és csúcssebessége egy autónak, ha mondjuk csak a sofőr ül benne, ahhoz képest, ha vontat egy lakókocsit, van rajta tetőcsomagtartó, visz még három utast, és teli van a csomagtartó is. A vadászgépeknél sincs ez másként, amíg külső függesztéssel hordozzák a fegyverzetet és sok minden mást is.

A vadászgépek csúcssebessége, hatósugara és számtalan más paramétere egészen szélsőséges értékek között változhat. Repülőgépes körökben viszonylag ismert közmondás, hogy ne autóskártyás módon ítéljen meg az ember dolgokat, vagy a mi esetünkben ez inkább repülőskártyás módon.

Egy repülőgép minden maximális paramétere között nem ÉS, hanem VAGY kapcsolat van, de még ez is nagyon enyhe közelítése a valóságnak. Lássuk tehát sorban a fő tényezőket, majd azok bemutatása után néhány konkrét, számszerű példát, hogy az elmélet mellett lássuk a gyakorlatot is.

A tolóerő

A tólóerő alapvetően befolyásolja a gyorsulást, emelkedő- illetve forduló képességet. A hajtóművek tolóerejét a források szinte kizárólag csak a fékpadi értékkel mutatják be. Ez egy mérőszámos mutató, ami ráadásul több tényező miatt torzít, emiatt részben fals információkat ad egy repülőgép repülési teljesítményéről, ha azokat össze kívánjuk hasonlítani. Mi a probléma vele?

• Első körben alapvető hiányossága, hogy nem a repülőgépbe épített állapotban kifejtett tolóerő értéket mutat. A repülőgép szívócsatornájának hatása hiányzik, a fékpadi mérések során e nélkül mérik a tolóerőt.
• A légkör sűrűsége és hőmérséklete nem állandó még tengerszinten sem, nemhogy eltérő repülési magasságon. A magassággal csökken a levegő sűrűsége és hőmérséklete is. A fékpadi mérés ehhez képest jellemzően tengerszinten történik.
• Minél nagyobb sebességgel halad előre egy vadászgép, úgy növeli a beáramló levegő a tömegét a növekvő relatív sebesség miatt. Emiatt a szívócsatorna képes elősűríteni a beáramló levegőt, így a tolóerő függ a repülőgép sebességétől. A fékpadon meg ugye áll a hajtómű...

A diagramon az F-15A vadászgép F100-PW-100 hajtóművének tolóerő görbéi, vagy szakszerűbben tolóerő karakterisztikái vannak. Ezeken jól látszik a felsorolt tényezők hatása.

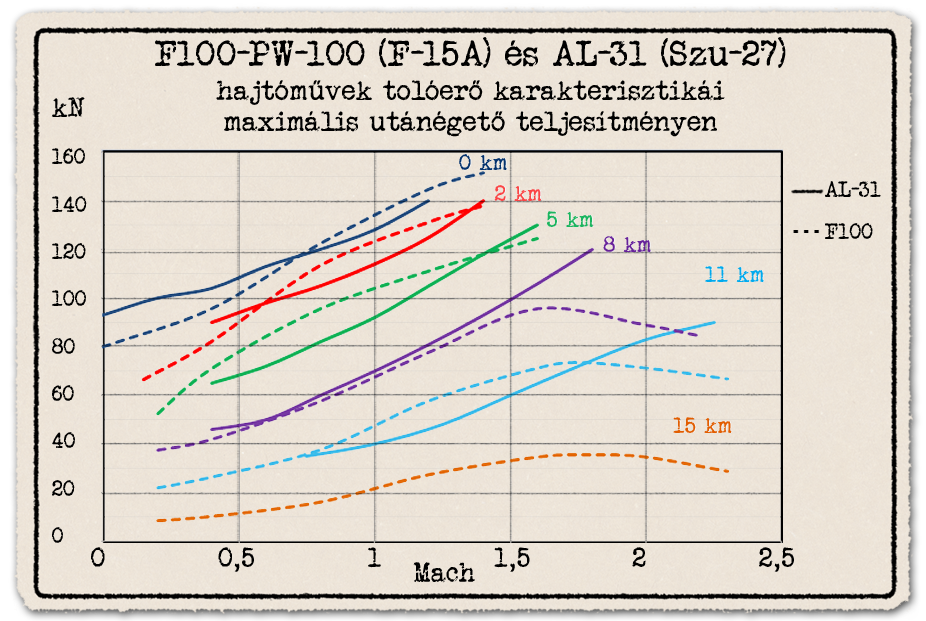
• Az F100 hajtómű fékpadi tolóereje utánégető nélkül maximálgázon 65 kN, utánégetővel 106 kN a prospektus adatok szerint. Ehhez képest a diagramon 0 km/h sebességénél tengerszinten 80 kN a tolóerő maximális utánégetéssel. Tehát a fékpadi értékhez képes számottevően, 25 százalékkal alacsonyabb. A szívócsatorna okozza ezt az eltérést, hiszen mindkét esetben a hajtómű a földön áll, a sebesség 0.
• Tengerszinten 1 Mach, vagyis hangsebességnél a tolóerő 133 kN, fékpadinál 25 százalékkal nagyobb, a tengerszinten álló helyzetben mérthez képest 66% (!) százalékkal magasabb.

Már egyetlen hajtóművet vizsgálva is látszik, hogy a fékpadi tolóerő semmitmondó érték a valós helyzetek vizsgálatához, mert a tolóerő nem állandó. Azonban nem feltétlen változik azonos mértékben a tolóerő eltérő hajtóműnél sebesség és magasság függvényében, vagy a fékpadi tolóerőhöz képesti tolóerő csökkenés sem azonos. Az F100 hajtóművet összehasonlítva a szovjet Szu-27 AL-31F hajtóművével láthatjuk, hogy a karakterisztikák jellegre különböznek egymástól.

Kis magasságon, kis sebességnél az F100 hajtómű tolóereje kisebb, mint a szovjet hajtóműé, viszont a hangsebesség közelében 5 kilométer magasságig már az F100 tolóereje a nagyobb. Úgy, hogy az F100 fékpadi, illetve 0 és kis sebességnél mért tolóereje is kisebb. Na, ehhez képest légiharc közben mégis lehet azonos, sőt nagyobb a tolóerje a fékpadi érték szerint kisebb tolóerejű hajtóműnek.

Kis sebességen a fékpadi tolóerőhöz képest az F100-zal összevetve arányaiban nagyobb a tolóerő csökkenése a szovjet hajtóműnek. Az AL-31 fékpadi tolóereje 134 kN, amihez képest az álló helyzetben mért tolóerő 93 kN, kb. 30 százalékkal alacsonyabb.

Már ebből is látszik, hogy ha valaki autóskártyáshoz módszerhez képest alig eltérő módon hasonlítja össze a
Szu-27 és F-15A vadászgépeket mekkorát tud tévedni. Mert hiába nagyobb az AL-31 fékpadi tolóereje 26%-kal, mint az F100 hajtóműé, ettől még a légiharc jellemző sebességtartományában, hangsebesség közeli tartományban az F100 és az AL-31 tolóereje lényegében azonos. Csak éppen nem mindegy, hogy az két
AL-31 egy olyan vadászgépbe van építve, aminek az üres tömege majdnem 4 tonnával több, mint az F-15-é. A fékpadi értékkel és 3-4 tonna üzemanyaggal számolva a tolóerő/tömeg arány nagyjából azonos lenne, csak a valóságban ugye nagyon nem ez a helyzet.

A tolóerő karakterisztika görbék ismeretében válik érhetővé, hogy laikusok és sajnos a szakma által használt tolóerő/tömeg arány önmagában félrevezető, mert azok a fékpadi értékeken alapulnak. Emiatt még további feltételekkel is legfeljebb csak egy becslésre alkalmasak. Ráadásul azt sem mutatja meg, hogy a tolóerőnek mekkora légellenállást kell legyűrnie. Nem csak a repülőgép tehetetlensége számít, hanem annak légellenállása is. Ezek kombinációja határozza a maximális sebességet és a gyorsulást is. A tolóerő görbék azt is megmutatják, hogy a hajtóművek teljesítménye a repülési magassággal csökken. A csúcssebességek bemutatásakor erre majd emlékezzünk vissza.

Még egy megjegyzés a margóra. Nagyon kevés hajóműről áll rendelkezésre ennyire részletes adat. Igaz, hogy ez csak két hajtómű, de mindkettő kétáramú gázturbinás, vagyis turbofan kialakítású.[1] Egy nagyon elkent becslésre a két görbe átlaga felhasználható, hogy a vadászgépek tolóereje átlagosan mennyit változik a fékpadi értékhez képest a 0-1,5 Mach tartományban adott magasságon. Néhány különleges vadászgépet leszámítva, azok életük kb. 98-99 százalékát hangsebesség alatt töltik tehát az interpolációnak azért van értelme.

Légellenállás

Na, akkor lássuk az egyenlet másik oldalát, hogy mi az, ami a tolóerőnek úgymond ellen tart. A repülőgépek légellenállása több komponensből tevődik össze, ezek a következők:

1. A homlokfelületéből és alakból adódó légellenállás. Lehet egy alapformának alacsony a légellenállás tényezője, de ha maga a felület nagy, akkor az abszolút légellenállása is nagy lesz. Leegyszerűsítve, két eltérő méretű gömb légellenállás tényezője lehet azonos, de a nagyobb méretű tárgy légellenállása a mérete miatt nagyobb.
2. A repülőgép felületén ébredő „súrlódás” jellegű légellenállás, vagyis a felületi ellenállás. Ez lényegében ahhoz hasonló, mint amikor két szilárd felület csúszik egymáson, csak itt a repülőgép és a környező levegő közötti „elcsúszás” okozza a légellenállás erőt. (A fizikára fogékonyabbak számára ezt hívjuk csúsztató feszültségnek.)
3. Interferencia ellenállás. A repülőgépen levő függesztményeknek és függesztő-berendezések légellenállása külön-külön kisebb, mint együtt a közös, indukált légellenállása. Például egy autó esetén a tetőcsomagtartó és az autó együttes légellenállása nagyobb, mint külön-külön.
4. Hullámellenállás, ez transzszonikus és szuperszonikus tartományban válik hangsúlyossá, lásd később.
5. A repülőgép állásszögéből eredő légellenállás, mivel vízszintes repülés esetén is szükséges felhajtóerő előállítása, ami légellenállással jár, ennek bemutatását szintén lásd később.

A légellenállás komponenseinek egymáshoz képesti arányait vízszintes repülés közben a következő diagramon láthatjuk. Az ábra csak nagyságrendek érzékeltetésére alkalmas, egy erősen elkent átlagot mutat be. Az arányok számottevően eltolódhatnak az adott repülőgéptől a hordozott fegyverzet mennyiségétől és a tömegétől is

A felsorolt ellenállás komponensek közül az első három laikusként is jól érthető, az ötödikre majd a felhajtóerő előállításnál térünk vissza. A hullámellenállás kifejtése, ami bővebb magyarázatot érdemel, ez hangsúlyos a szuperszonikus sebesség tartományban. Ennek bemutatásához egy analógiát hívunk segítségül.

A hajók esetén alapvetően két részre lehet bontani azok közegellenállását. A súrlódási és alakból adódó ellenállásra, illetve a hullámellenállásra. A hajóknál a hullámellenállás növekedés látványosan látszik, ez a sekélyvízi hullámterjedés, ami a víz sűrűsége, illetve viszkozitásából adódik, a hajó orránál és a hajótest mellett elhaladó és leváló hullámokon.

A levegőben haladó járművek esetén is létezik ez jelenség, hiszen a levegő is közeg, benne is van a zavarásnak terjedési sebessége, ez a hangsebesség, ami tengerszinten kb. 340 m/s. Ez csak nagyobb sebességnél, a hangsebességhez közeledve, illetve azt átlépve válik hangsúlyossá. Ez végtelenül leegyszerűsített és pontatlan analógiája a valóságnak, de a célnak megfelel, hogy értsük, hogy van másféle ellenállás is, mint súrlódás és homlokellenállás.

A vadászgépeknél a hullámellenállás két sebességtartományban játszik kritikus szerepet. A hangsebességhez közeledve, amikor a lökéshullámok még függőlegesek, illetve a hangsebesség elérésekor és azt meghaladva, amikor a repülőgép körül kialakuló lökéshullám-rendszer kúp alakot formáz meg. Ezek a hullámok Schlieren-optika[2] segítségével jól láthatóvá tehetők. Érdekesség, hogy hangsebesség felett a lökéshullám kúpszöge[3] csakis a haladási sebességtől függ, a tárgy formájától teljesen független.[4]

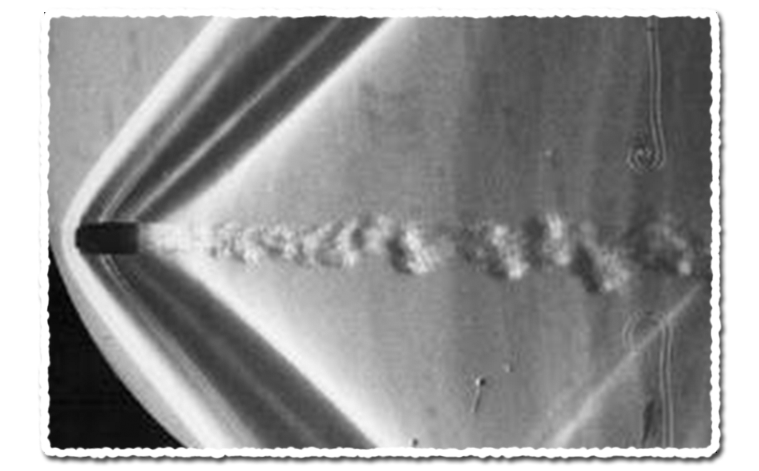
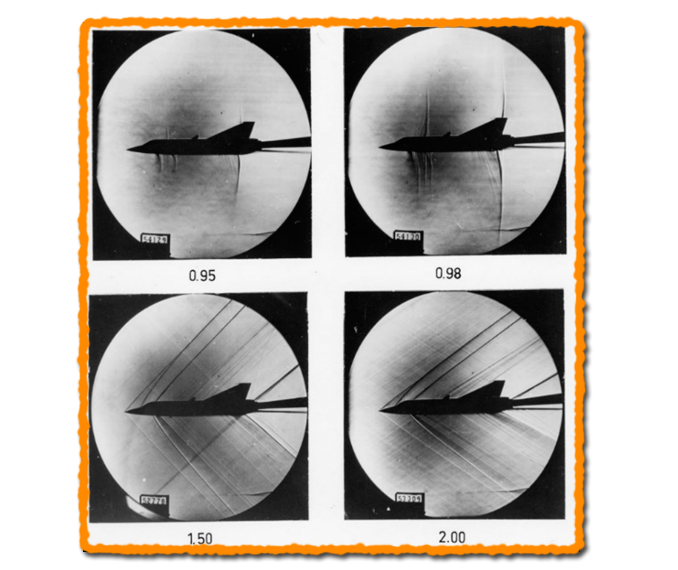
A hullámellenállást a repülőgép hossz mentén, az áramlási főirányba eső változó keresztmetszet-változása határozza meg, az adott sebességnél a lökéshullám szöge által meghatározott kimetszett szeleteknek megfelelően. Mivel a lökéshullám kúpszöge változik a sebességtől függően, emiatt repülőgépek hullámellenállása azok formájától és az aktuális sebességtől is függ. Ennek az eloszlásnak van egy fizikai-matematikai optimuma, aminek minél jobb közelítése a cél. Minden ettől való eltérés növeli a hullámellenállást a minimumhoz képest. Az ábrán látható, hogy hogyan kell elképzelni adott forma esetén ezen „szeletek” elkészítését. Ez azt is jelenti, hogy a hullámellenállást csak egyetlen sebességre lehet minimalizálni egy adott geometriával. Ezt a fizikai jelenséget hívják területszabálynak, a kimetszett terület nagyságának a jelentősége miatt.

 Az YF-23 technológiai demonstrátor repülőgép rajzán látszik a területszabály alkalmazása és figyelembevétele. A rajz felső részén látható az adott Mach szám esetén kijelölt ideális és a repülőgép formája által megvalósított keresztmetszet eloszlás, a „cross section area plot”. Látható, hogy egyik sebességnél sem az ideális, de egészen jól közelíti azt.

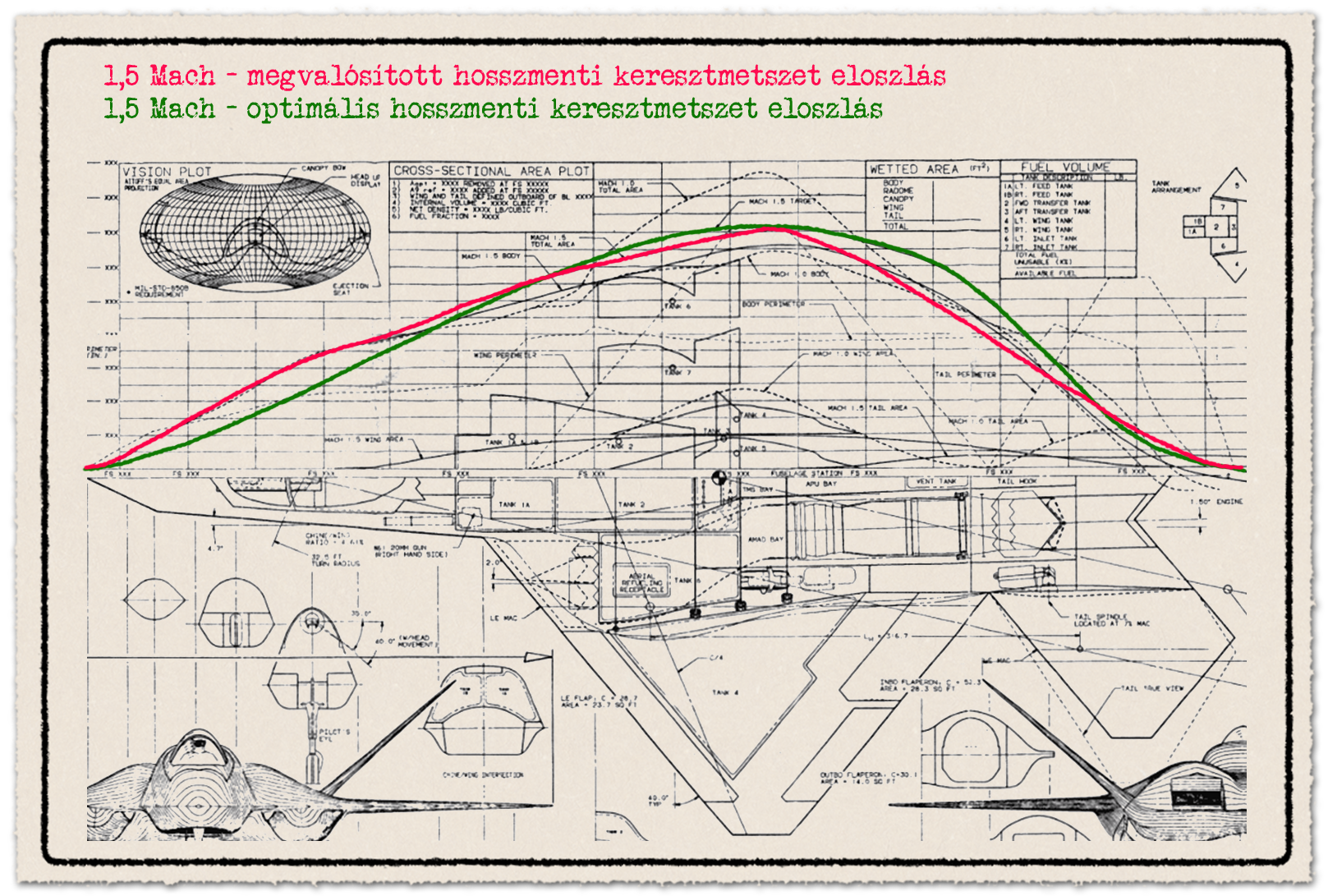
A területszabály következménye, hogy belső fegyvertérrel rendelkező lopakodó vadászgépek szuperszonikus légellenállása nagyon kedvező lehet, ha tervezés során a területszabály alkalmazása helyesen történt. A fegyverzet nem változtatja meg a hosszirányú keresztmetszet eloszlást, sőt, a repülőgép homlokfelületét sem növeli.

A hagyományos vadászgépeknél már szerény mennyiségű külső függesztéssel hordozott fegyverzet is számottevő mértékben rontja a szuperszonikus teljesítmény paramétereket. Emiatt volt az, hogy a korai készeres hangsebességre képes vadászgépek jellemzően csak két darab és nem túl nagy tömegű légiharc-rakétát hordoztak. Erre jó példa a szovjet MiG-21-F13 és angol English Electric Lightning. Csak így volt elérhető a kívánt nagy csúcssebesség.

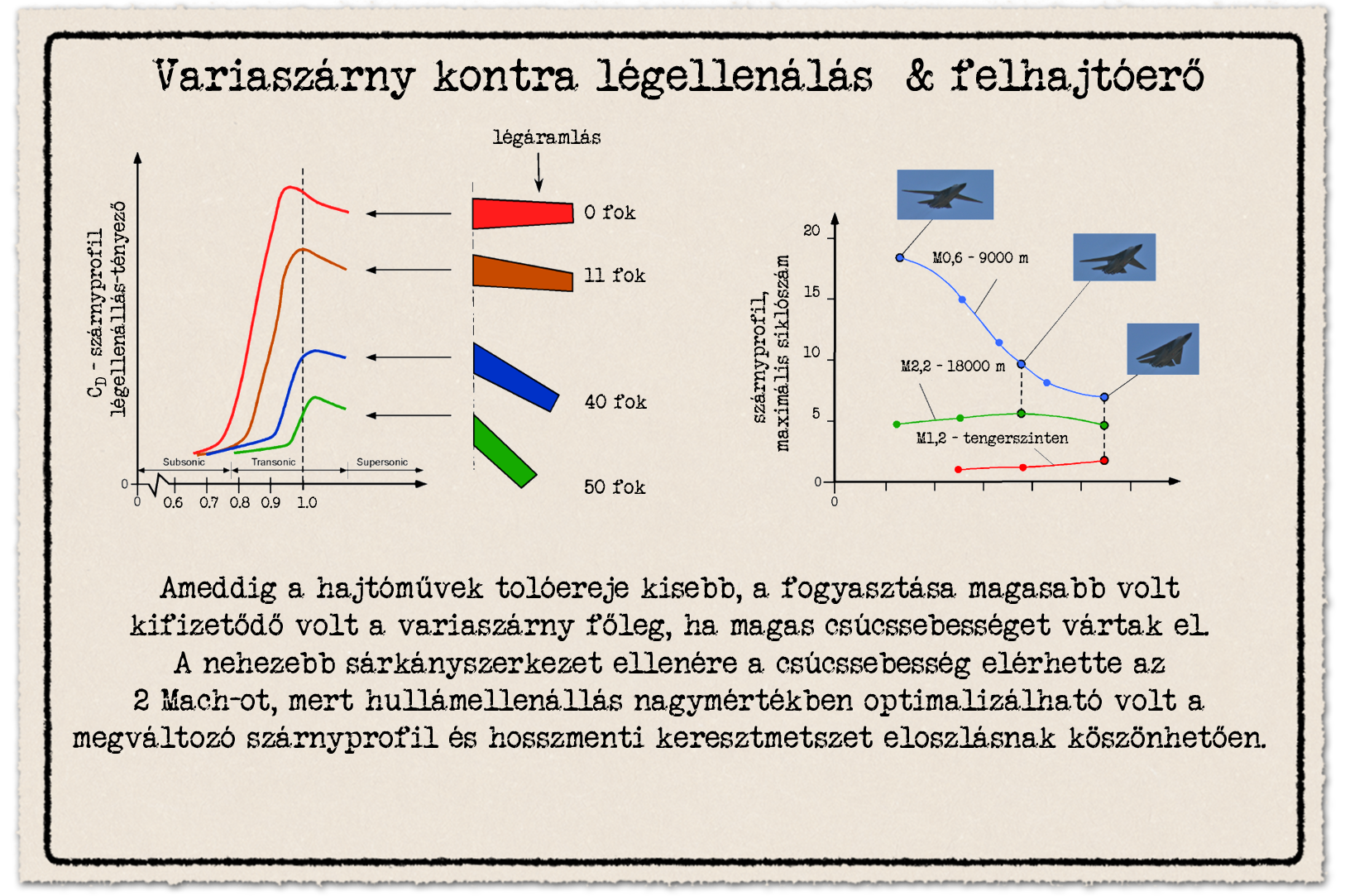
Részben a területszabály miatt volt egy ideig népszerű a változtatható szárny-nyilazású harci gép koncepciója. Ezt használta például az F-14, vagy a csatornán már taglalt MiG-23 is, de a szuperszonikus sebességre képest Tu-22M és a Tu-160 bombázó is.[5]. A kisebb csapásmérők közül az F-111, Szu-24 és a Tornado is ezzel a megoldással rendelkezik. A szárny nyilazási szöge nem csak a hosszmenti keresztmetszet eloszolást, tehát a hullámellenállást, hanem homlokfelületet is és a szárny áramlási irányába eső húrhosszt is megváltoztatja, tehát ettől az áramlási irányhoz képest még a szárnyprofil is megváltozik. Lényegében, minta repülés közben kicserélnék a repülőgép szárnyát. Maximális nyilazásnál az F-14 majdnem, mintha egy deltaszárnyú vadászgép lenne, addig a legkisebbnél erős túlzással vitorlázógép szárnyaihoz hasonló, ami látunk.

A variaszárnynak köszönhetően egy repülőgép képes alacsony leszálló sebességet elérni úgy, hogy akár a 2,5 Mach elméleti csúcssebessége is lehet, még relatíve szerény tolóerővel is, köszönhetően a kisebb homlokfelület és eltérő hullámellenállásnak. Ez amúgy megint jól mutatja, hogy mennyire korlátozottan használható a tolóerő/tömeg viszonyszám a teljesítmény leírására, lásd majd később konkrét példán.

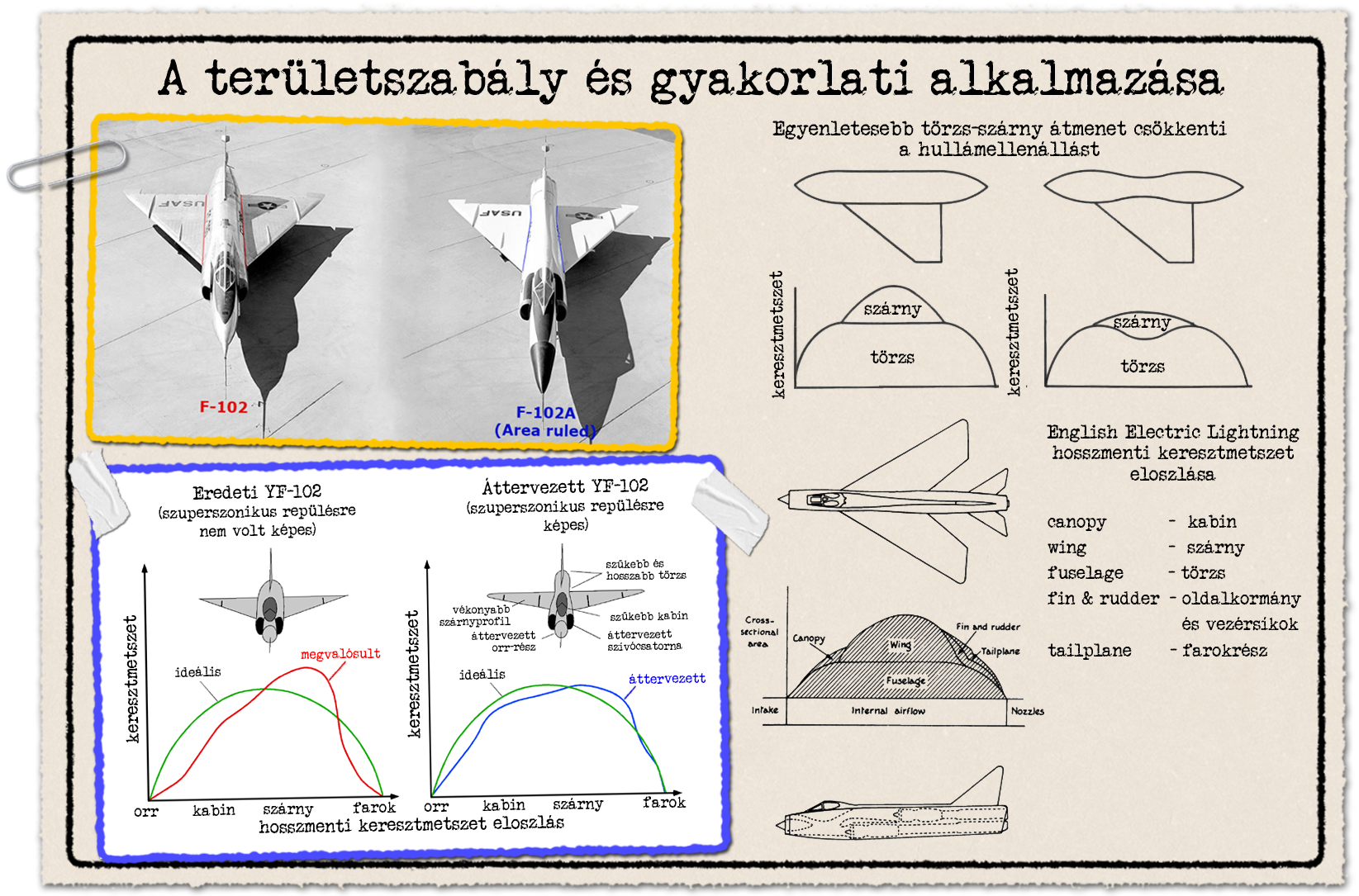
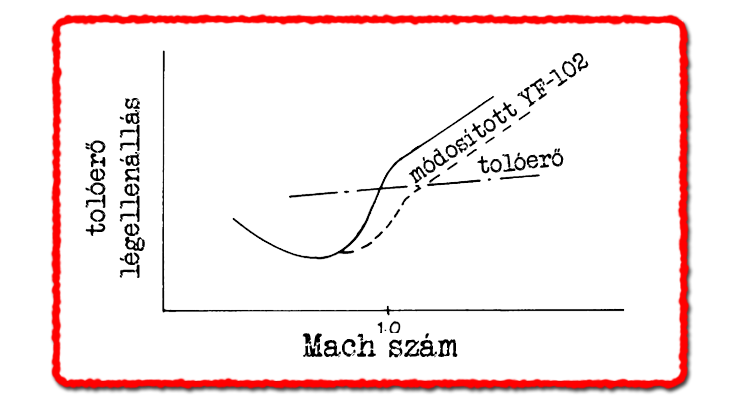
A területszabály alkalmazásának nyilvánvaló jelei az F-102 és F-5 vadászgépek esetében jól látszanak, kezdjük az első típussal. A hullámellenállás fontosságának ikonikus példája az F-102 Delta Dart honi légvédelmi vadászgép[6]. A szuperszonikus sebességre tervezett vadászgép eredeti formájában még a hangsebességet sem volt képes átlépni. A területszabály megértése és helyes alkalmazásával sikerül végül hangsebesség feletti vadászgépet faragni belőle úgy, hogy az alapforma radikálisan nem változott. A szárnyak által okozott keresztmetszet növekedést kompenzálták ki a törzs elvékonyításával, ezzel közelebb lett a keresztmetszet eloszlása az ideálishoz képest.

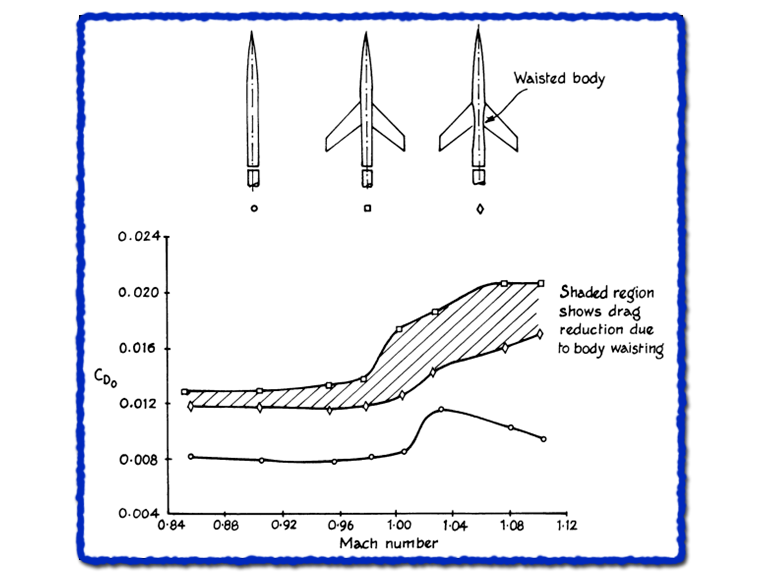
Lássuk egy egyszerű példán keresztül, hogy az elkeskenyítés mennyire komoly hatással bírhat. Az ábrán látható, hogy a légellenállás tényező hogyan alakul a lövedék, szárnyas lövedékforma, illetve elkeskenyített szárnyas lövedékforma esetén. A légellenállás akár 25-35%-kal is csökkenthető adott sebességtartományban. Ha ennyire kis változtatás hatása ekkora, akkor el lehet képzelni, hogy a repülőgépek külső függesztése mit okoz...

Az F-5 vadászgépnél is látható a területszabály alkalmazása, de nem csak magán a repülőgépen. A szárnypóttartályok emiatt nem egyenesek, hanem a területszabály szerinti optimalizált formával bírnak. A Mirage-2000 vadászgépen alkalmazott egyik póttartály változatnál ezért néz ki laikus szemek furcsán, hogy az nagyobb keresztmetszetről szűkül kisebbre. A póttartály önmagában ezzel rosszabb hullámellenállással bírna, de a repülőgép és a póttartály együttese ezzel mégis jobb eredményt ad.

A területszabály alkalmazása már hangsebességhez közeli tartományban is fontos. Emiatt vannak, a laikusok számára megmagyarázhatatlan dudorok a szárny kilépő élén pl. a Tu-95 bombázón, de még kereskedelmi utasszállító repülőgépeken is látható ilyen. Már a 0,8 Mach sebesség tartománynál is megéri plusz tömeget cipelni, mert a hullámellenállás annyival kisebb, hogy ettől a teljes légellenállás kisebbre adódik. A Concorde, kétszeres hangsebessége képes utasszállítónak a sorozatgyártott változatán a farokkúpot azért hosszabbították meg, mert a hullámellenállásra gyakorolt pozitív hatása miatt szintén megérte a nagyobb tömeg.

Az ábrán néhány repülőgép zero-lift to drag légellenállás tényezője látható a szubszonikus és szuperszonikus tartományban. Ez az a légellenállási tényező, amely nulla felhajtóerő mellett keletkezik. (Cd₀ vagy C_x0).

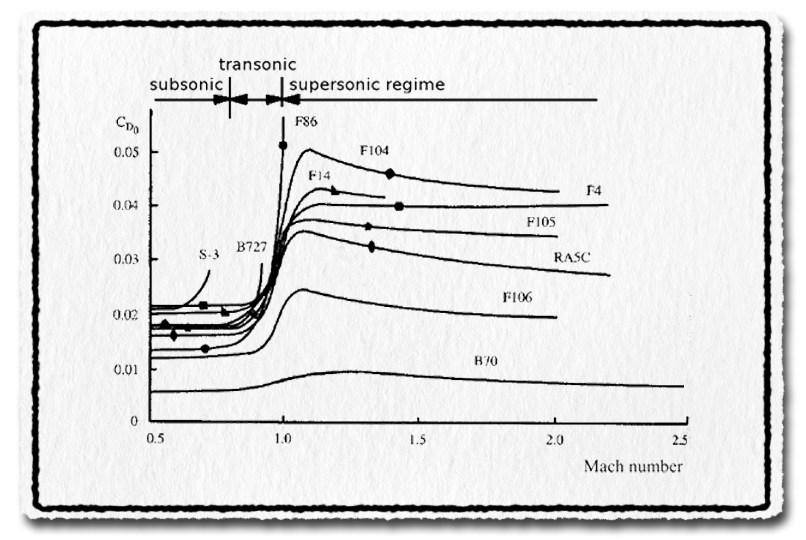
 A szuperszonikus repülés és lökéshullám két területen bír kiemelkedő fontossággal. Amikor a lökéshullám eléri a szárny belépőélét, akkor komoly vezethetőségi és stabilitási problémák jelennek meg, ezért ezt jellemzően igyekeznek elkerülni. Ez a repülőgép fizikai méretének és formájának helyes megválasztásával biztosítható, hogy adott sebességnél a lökéshullám ne érje el szárnyak belépő élét.

A másik a hajtómű szívócsatornákhoz kapcsolódik, aminek egyik fő feladata az, hogy kezelje a lökéshullámok által generált problémákat. A szívócsatornák alakjuknak köszönhetően befolyásolják a lökéshullámokat, függőleges lökéshullámrendszert állítanak elő a szívócsatornában.[7] Ez azt jelenti, hogy a légáramlat a hajtóműben akkor is hangsebesség alatti, de ahhoz közeli, amikor a repülőgép hangsebességnél gyorsabban repül. Ennek következménye a dinamikus elősűrítés, a repülőgép előrehaladásának köszönhetően, már az első kompresszor fokozat előtt a szívócsatorna eleje sűríti a beáramló levegőt.

Emiatt a szívócsatorna kialakítása korlátozhatja a repülőgépek maximális sebességét annak ellenére, hogy adott esetben pusztán tolóerő és a légellenállás paraméterek ellenére nagyobb csúcssebesség is elérhető lenne elvi szinten. Erre kiváló példa az F-35 vadászgép család. Pusztán a fékpadi tolóerőt és a repülőgép tömegét nézve a csúcssebességnek bőven 2 Mach felett „kellene” lennie, legalábbis laikus szemmel nézve. A fix keresztmetszetű szívócsatorna és egyéb követelmények miatt adminisztratívan van korlátozva a csúcssebessége 1,6 Mach értékre. Viszont ettől még az F-35 gyorsulása a transzszonikus és alacsony szuperszonikus tartományban a vadászgépeknél teljesen megszokott tartományban van. A 2 Mach feletti sebességtartomány lényegében csak változtatható geometriájú szívócsatornával érhető el.

Érdekesség, de nem kapcsolódik közvetlenül a témához, hogy szubszonikus repülési sebességgel is a szárny felső felületén az áramlás sebessége nagyobb, mint a repülési sebesség, így helyi áramlási sebesség meghaladhatja az 1 Mach-ot. Ennek az áramlásnak a lefékeződése hoz létre az áramlásra merőleges lökéshullámot. Azt a szubszonikus repülési sebességet, amelynél a szárny feletti áramlási sebessége eléri az 1 Mach értéket, kritikus Mach számnak hívjuk. Ezt a jelenséget amúgy kereskedelmi utasszállító repülőgépnél is meg lehet figyelni a szárny felett.[8]A lökéshullám felületén a levegő törésmutató megváltozik, emiatt látható a jelenség. De ettől még a repülőgép hangsebesség alatt repül. Az F-18 és F-35-ről készült fotókon láthatók ezek a lökéshullámok.

A repülőgépre ható erők, felhajtóerő

A következő lépés annak megértése, hogy hogyan állítják elő a felhajtóerőt, ugyanis ettől is függ a repülőgép légellenállása is. Kezdjük az állásszög fogalmával. A geometriai állásszöget a repülőgépek szárnyprofiljának húrjához és a repülőgép haladási irányához képest határozzuk meg. A szárnyprofil húrja a belépőélt és kilépőélt összekötő egyenes, ennek bezárt szögét mérik a zavartalan közeg relatív áramlási sebességéhez képest. Ez látható a sematikus ábrán. A szárny alakja csak illusztráció, a szárnyprofilok ennél lényegesebben vékonyabbak a vadászgépeken, csak a szárny íveltségének bemutatása a cél. A korai szuperszonikus repülőgépek közül több típus is szimmetrikus szárnyprofilt használt, azok nem termeltek felhajtóerőt 0 fokos állásszög mellett, a nem szimmetrikus szárnyprofilok azonban igen.

Bármilyen légáramba helyezett test, ami állásszöggel bír a légáram haladási irányához képest, azon felhajtóerő ébred legyen az bármennyire nem áramvonalas. Igen, még egy téglán is ébred felhajtóerő. De bárki megtapasztalhatta már ezt, aki mozgó kocsiból kitette a tenyerét élével és forgatta azt. Igen jól érződik a kar csapkodásán, hogy ott bizony erő ébred.

Ez azért fontos, mert bár a repülőgépek szárnyain ébred a felhajtóerő többsége, de ez nem jelenti, hogy csak azokon. A korai vadászgépeken a törzs jellemzően hengeres vagy ellipszis keresztmetszetű volt, amihez szárnyakat csatlakoztattak, de ezek élesen elváltak egymástól. Ilyen például klasszikusan a MiG-21 vagy az F-4 Phantom II. Az F-14 megjelenése óta viszont már az úgynevezett lifting body koncepció használatos, ahol a géptörzs és a szárnyak nem válnak el élesen egymástól, ennek köszönhetően a hatalmas méretű törzs szekció részben a szárnyak meghosszabbítása. Bár lényegesen rosszabb hatásfokkal, de a hatalmas felület miatt egyes állásszögeknél akár a teljes felhajtóerő 20-25%-is a szárnyakon kívüli területeken ébred.

A szárnyak alapvető működési elve leegyszerűsítve, hogy az állásszöggel rendelkező szárny két oldala között nyomáskülönbség jön létre, ez biztosítja a szükséges felhajtóerőt. Nem szimmetrikus szárnyprofilok 0 fokos állásszögnél is termelnek már felhajtóerőt. Adott sebességnél nagyobb felhajtóerő előállítása mindig nagyobb légellenállással is jár, hiszen ahogy nő az állásszög, úgy nő az áramlásra merőleges homlokfelület is.

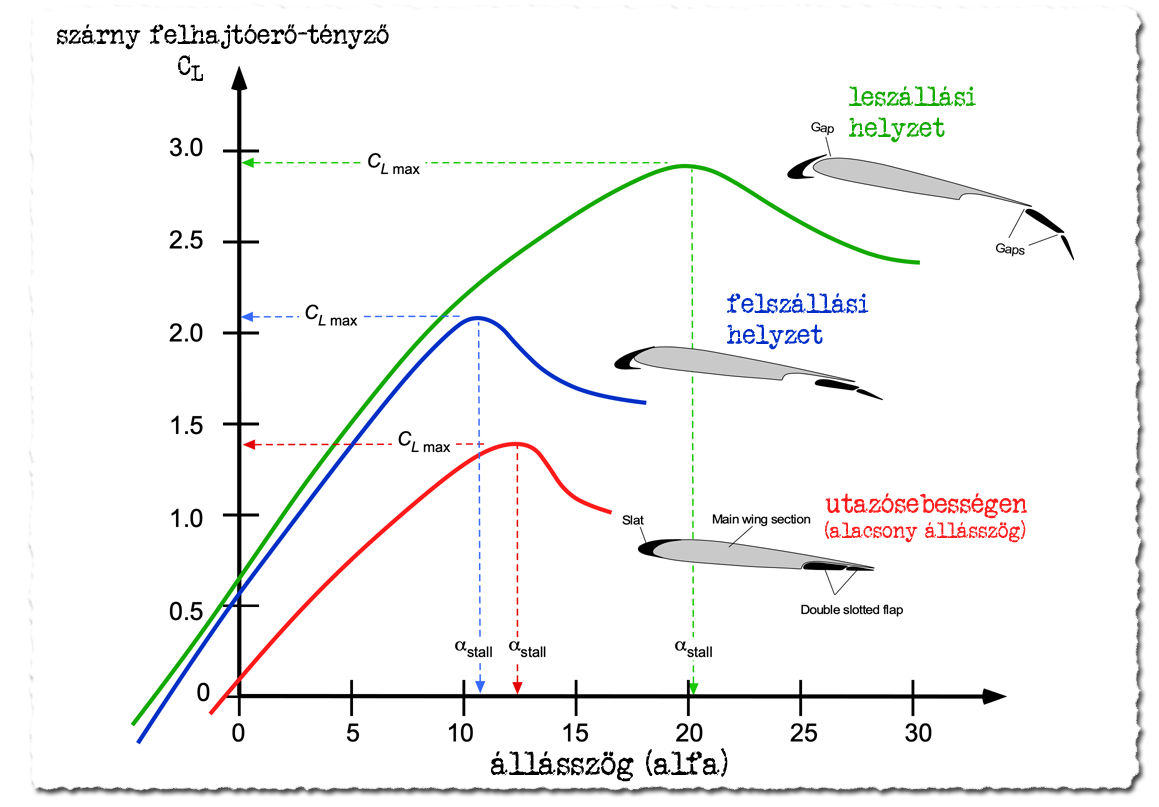
Az két ábrán átlagos szárnyprofilok felhajtóerő- (C_L vagy C_y) és ellenállás-tényezői (C_D vagy C_x) láthatók. Növekvő állásszög, az alfa (α) mellett egyre nő a felhajtóerő tényező, azonban egy adott állásszögnél a felhajtóerő növekedése megáll, majd csökkenni kezd. Ezt nevezzük kritikus állásszögnek, ahol a szárny úgymond átesik az áramlási viszonyok drasztikus megváltozása miatt. Ez már a szárny normál üzemi tartományán kívül esik. Azon az ábrán, ahol a légellenállás tényező is fel van tüntetve látható, hogy az állásszög növekedésével a légellenállás-tényező is nő a felhajtóerő-tényező mellett. Erre emlékezzünk, de NAGYON erősen, amikor repülőgépek irányváltoztatási képessége lesz a téma. A két tényező hányadosa a kritikus állásszögnél kicsit kisebb állásszög tartományig kedvező marad, ahol hirtelen drámaian megnő a légellenállás. A felhajtóerő-tényező és légellenállás-tényező hányadosa a siklószám.

A hasonló diagramoknál sokszor csak a pozitív állásszögekhez tartozó tartományt ábrázolják, de ettől még a viselkedés negatív tartományban érvényes marad, de nem azonos mértékben, legalábbis a nem szimmetrikus szárnyprofiloknál. A diagramon 0 fokos állásszögnél mutat felhajtóerőt, tehát nem szimmetrikus szárnyprofilt mutat be.

A repülőgépek vízszintes repülés esetén is mindig valamekkora állásszöggel repülnek, még ha az csak néhány fokos és szabad szemmel alig látszik. Vízszintesen haladáskor is szárnya és maga az egész géptörzs pozitív szöget zár be az vízszintessel. Amikor vadászgépek fejjel lefelé repülnek vízszintesen, akkor a normál helyzethez képest nagyobb állásszöggel szükséges repülni. Ennek oka látszik a diagramon. A nem szimmetrikus szárnyprofilokat arra tervezik, hogy pozitív állásszögeknél legyenek hatékonyak, ezért negatív állásszögnél azonos felhajtó erőhöz nagyobb negatív állásszög szükséges.

A felhajtóerő a felhajtóerő-tényezővel, a repülőgép haladási sebesség négyzetével, a szárnyfelülettel és a levegő sűrűségével arányos. Minél nagyobb a sebesség, annál több felhajtóerőt generál a szárny és persze az egész sárkányszerkezet is. Minél nagyobb a felülete, annál nagyobb felhajtóerő ébred rajta azonos siklószám esetén. Emiatt van az, hogy kis sebességnél, pl. leszálláskor nagyobb az állásszög, akár 10 fok körüli is lehet. Utazósebességen ezzel szemben a repülőgépek 2-5 fokos állásszöggel repülnek, de ez is sok tényezőtől függ. Szintén emiatt van, hogy nagyobb magasság és ritkább légkörben nagyobb állásszöggel kell repülni vízszintes repülésnél.

Még egy apró megjegyzés, a felhajtóerő tényező nem állandó, az függ magától a sebességtől és részben a levegő hőmérsékletétől, sűrűségtől és a viszkozitástól is.

Hogyan repül?

Három tengely körüli kormányzás

Most már ismerjük a gépre ható fő erőket, amivel lehet dolgozni, de ebből hogyan lesz irányított repülés? Hogyan repül vízszintesen egy repülőgép és hogyan változtat irányt?

Az már láttuk, hogy felhajtóerőt tud előállítani a repülőgép, ami az állásszögtől függ, a tolóerőt vízszintes repülésben a hajtómű biztosítja, amire süllyedésben a gravitáció rásegít. A repülőgépet lassítja a légellenállás, a gravitáció a Föld felé húzza a gépet, ez emelkedéskor egyben lassítja is a gépet. Ezekkel az erőkkel lehet játszadozni.

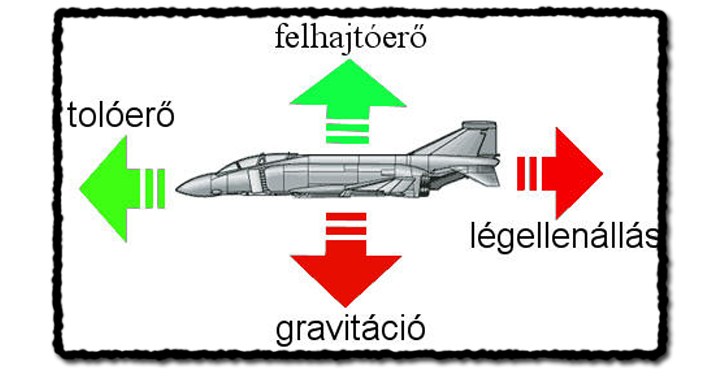
(Nagyon egyszerűsített ábra, mert a toleró, a felhajtóerő és a légellenállás sem tisztán függőleges és vízszintesek, de a lényeg látszik. Ezen fő hatások és azok erő komponensei a lényegesek.)

A cél a repülőgép állásszögének, illetve a térbeli helyzetének irányított változtatása, a repülőgép saját három tengely körüli forgatása. Ezzel érhető el, hogy a felhajtóerő a kívánt irányban mutasson, ezzel lehet a repülőgép sebesség vektorának, tehát haladási irányának megváltoztatása, illetve így állítható be a kívánt állásszög. Az ehhez szükséges kormányfelületek, a következők:

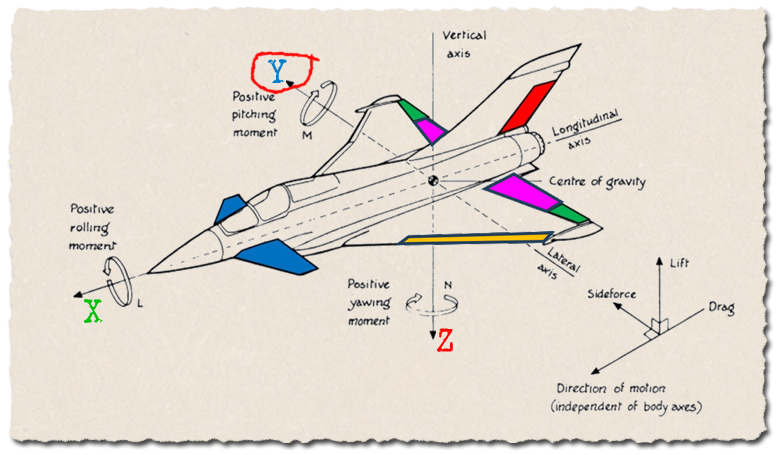
• A hossztengely körüli forgást, ez az X tengely, az orsózást (roll) csűrőkormányokkal lehet elérni, az ábrán ez a zöld színű rész (aileron).
• A kereszttengely körüli forgást, ez az Y tengely, a bólintást (pitch) a magassági kormány, vagyis a stabilizátorok használatával (elevators) lehet elérni, ez a kék színű rész. [9] Kacsa-vezérsíkkal rendelkező gépek esetén az látja el ezt a feladatot.
• A függőleges tengely körüli forgást, ez a Z tengely, a legyezőmozgást (yaw) az oldalkormánnyal (rudder) lehet elérni, ez a piros színű az ábrán.

A kormányfelületek kitérítésekor azokon erő ébred, hiszen megváltoztatják a légáram irányát. Az erők a súlyponttól távolabb ébrednek, ezért azok nyomatéka képes forgatni a gépet a három tengelye körül attól függően, hogy melyik és mekkora mértékben van kitérítve. Mivel a kormányfelületek a repülőgép súlypontján nem átmenő erőkkel generálnak nyomatékot és indukált ellenállással megváltoztatják az egész repülőgép körül az áramlást, ezért mind a három kormányfelület egyidejű használata szükséges a legtöbb esetben a kívánt manőver eléréséhez.

A fent felsorolt három kitéríthető kormányfelületen túl további szárnymechanizációval is rendelkezhetnek a vadászgépek. Ilyen például fékszárny (flap), ezek az ábrán magenta színnel vannak jelölve. A fékszárny kis sebességű, nagy állásszögű repülésnél használatos, a szárnyon ébredő felhajtóerőt növelik meg adott állásszögön. Mondhatni ez is egy fajta variaszárny, csak annál sokkal egyszerűbb és korlátozottabb a használata. Ez a klasszikus variaszárnnyal ellentétben csak a szárny íveltségét változtatja meg. Tehát olyan, mintha egy másik szárnyprofillal rendelkező szárnya lenne a repülőgépnek. Nem csak a szárny felhajtóerő tényező karakterisztika jellegét változtatja meg, hanem a kritikus állszöget is növeli jellemzően a szárny íveltségének a növelése.

Egyes vadászgépek rendelkeznek orrsegédszárnnyal (leading edge flap),^[10] ez sárga színű az ábrán. A példaként szereplő F-15 nem, de például F-16 rendelkezik ilyenekkel. Ez kitolja a vékony profilú szárnyak használható állásszög tartományát, késleltetve az áramlás leválását, az átesést. A fékszárnnyal ellentétben az orrsegédszárny nagy sebességű, nagy túlterhelésű, nagy állásszögű manőverek közben is ki lehet térítve.

A törzsféklap (airbrake) a legegyszerűbb, egyszerűen arról van szó, hogy kisebb-nagyobb lapokat kitolva növelik meg a repülőgép légellenállását, erre például leszálláskor lehet szükség. Két eltérő megvalósítás látható az F-15 és F-16 vadászgépeken.

Egyes repülőgépeken a magassági- és csűrőkormányok összevontan működnek, ilyenkor elevon-ról beszélünk, az elevator és aileron szavak összevonásából ered ez a megnevezés. Jellemzően a deltaszárnyú és csupaszárny gépeknél használatos ez a kialakítás. Ez az funkció összevonás féklapok (flap) és oldalkormány (aileron) esetén is lehetséges, ekkor „flaperon” megnevezés használatos, ilyen van például az F-16 típuson.

Mi a jellemző állásszög tartománya a vadászgépeknek? A 4. generációs vadászgépek függesztmény nélkül nagyjából legfeljebb 26-40 fok körüli állásszöggel képesek repülni, csak ezen tartományon marad meg a három tengely körüli kormányozhatóság. A 20-22 fok feletti állásszög tartomány lényegében csak kis sebességű manőverek közben érhető el. Nagyobb sebesség és kis magasságon már sokkal kisebb állásszöggel is elérhető a repülőgép túlterhelhetőségének a maximuma.

Fontos megérteni, hogy nem a kormányszervek állítják elő a felhajtóerőt, azok csak azért felelnek, hogy a levegő áramlási sebességéhez képest a kívánt állásszög és irányban álljon a repülőgép. Ezek hatásossága természetesen függ a sebességtől és az állásszögtől is. Kis sebességnél nem képesek olyan gyorsan forgatni a repülőgépet az adott tengelyek körül, mint nagyobbnál, mert kisebb az ébredő légerő. Ezen felül részben le is lehetnek árnyékolva a nagysebességű turbulens áramlás elől a nagy állásszögű manővereknél. Ezért van az, hogy kis sebességű, de nagy állásszögű manővereknél maga a három tengely körüli forgási sebessége korlátozott a nagysebességű repüléshez képest. A sebesség növekedésével egy ponton túl a kormányszervek maximális kitérítése korlátozva van, mert akkora erő ébredne azokon, hogy akár károsodhatna a szerkezet.

Hogyan változtat irányt a repülőgép?

Oké, oké, de hogyan változtat irányt egy repülőgép? A repülőgépek mozgásának megértéséhez szükséges megismerkedi a középiskolás fizikán túli mozgástannal. Lényegében már eddig is annak bevezetése történt meg a fentiekben, hiszen a három tengely körüli forgás nem elemi tömegpontként való leírása a valóságak. A repülőgép viselkedését pontszerű testként kezelve nem lehet leírni, mert a saját három tengelye körüli helyzete is alapvető tényező a repülőgép haladási irányához és sebességéhez képest.

A fentiek ellenére kezeljük repülőgépet most egy elemi tömegpontként. Egyenes vonalú, állandó sebességű repülésnél a tolóerő, a légellenállás, a felhajtóerő és a gravitáció kiegyenlítik egymást, tehát a sebesség vektor a tömegpont haladási irányába mutat. Szuper. Ha egy tömegpont haladási irányát szeretnénk megváltoztatni, akkor mi szükséges hozzá? Erő. Na ennek az erőnek az előállítása feladat.

A tömegpontos egyszerűsítéssel élve, a sebességvektorhoz képest eltérő irányú erővel változtatható meg a tömegpont sebességvektora. Ezt célszerűen merőleges irányú erővel állítjuk elő, hiszen az gyorsítja legjobban a testet eltérő irányba. A haladási irányához képest nagy oldalirányú erőt a repülőgép csak egy módon képes előállítani, nagyobb felhajtóerő generálásával és annak megfelelő irányba forgatásával.

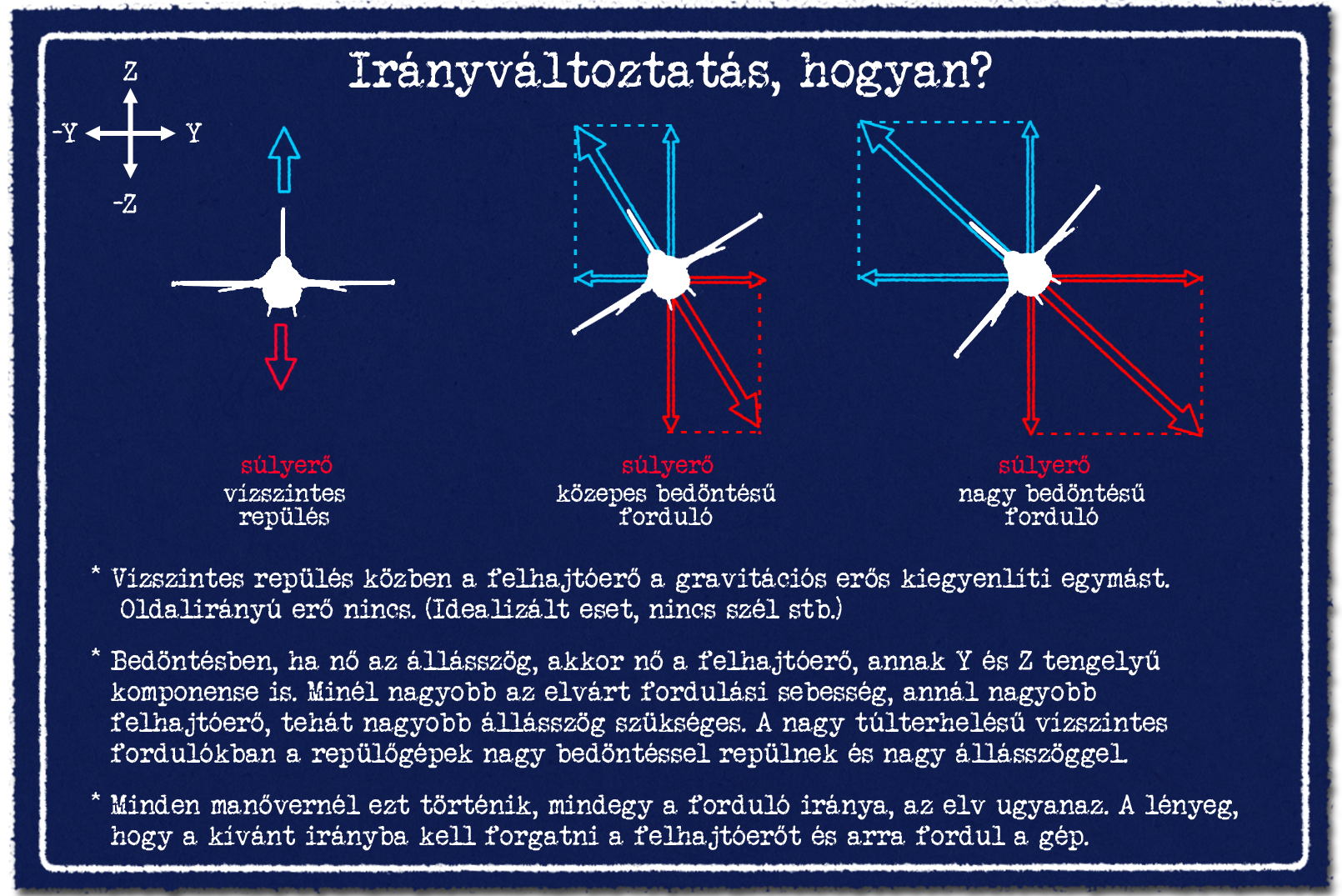
Az ábrán levő erők adott tengely irányú komponenseinek felbontásával érthető meg a hogyan. Vízszintes repülés közben a felhajtóerő a gravitációs erős kiegyenlíti egymást. Oldalirányú erő nincs. Ha a repülőgép a hossztengely körül elforog, tehát bedöntést végez a kormányszervek használatával, akkor azonos állásszög esetén a felhajtóerő nem változik, csak annak függőleges komponense már kisebb lesz, mint a gravitációs erő. Viszont a felhajtóerőnek immáron van oldalirányú, Y tengelyű összetevője is. Egy ilyen helyzetben a repülőgép haladási iránya változni fog, de süllyedni fog a vízszintes repülés állásszögével.

Viszont, ha megnöveljük az állásszöget, akkor nő a felhajtóerő, annak Y és Z tengelyű komponense is. Minél nagyobb az elvárt fordulási sebesség – ezt hívjuk forduló szögsebességnek – annál nagyobb felhajtóerő, tehát nagyobb állásszög szükséges. Emiatt van az, hogy a nagy túlterhelésű vízszintes fordulókban a repülőgépek erős bedöntéssel repülnek és nagy állásszöggel. Mert még a hatalmas felhajtóerő ellenére is, annak Z irányú komponense csak a gravitációval tart egyensúlyt, a nagyobb Y irányú komponense viszont a gép haladási irányát változtatja meg.

Minden manővernél ezt csinálja a repülőgép, teljesen mindegy a forduló iránya, az elv ugyanaz. Ha bedöntést nélkül növeli az állásszöget, akkor a gép nem a Z tengely, hanem az Y tengely körül forog, tehát a bólintási szöge nő, tehát emelkedni kezd. Mindig az a kérdés, hogy a tolóerő, a felhajtóerő, a légellenállás és a gravitációs erőknek mekkora komponense esik az adott tengelyekbe. Függőleges emelkedéskor például a gravitációs erő lényegében szinte azonos irányba mutat a légellenállás vektorral, tehát a légellenállás ÉS a gravitációs erő lassítja a gépet. A valóságban a felhajtóerő, különösen nagy állásszögeknél, nem merőleges a szárny húrhosszára, de maga az alapelv ettől szintén ugyanaz, ezek már csak az egzakt leírás finomságai.

https://youtu.be/eXaPfUs6sQw?t=1m13s

A bevágott videó részleten jól látszik, hogy G, vagyis a nehézségi gyorsulás értéke hogyan változik, amikor a gép kisebb és nagyobb túlterhelésű fordulókat hajt végre. Minél gyorsabban fordul, annál nagyobb a túlterhelés. Amikor a repülőgép 9G-s fordulót hajt végre, akkor a gép súlyának kilencszere a felhajtóerő azon komponense, ami a fordulóért felel.

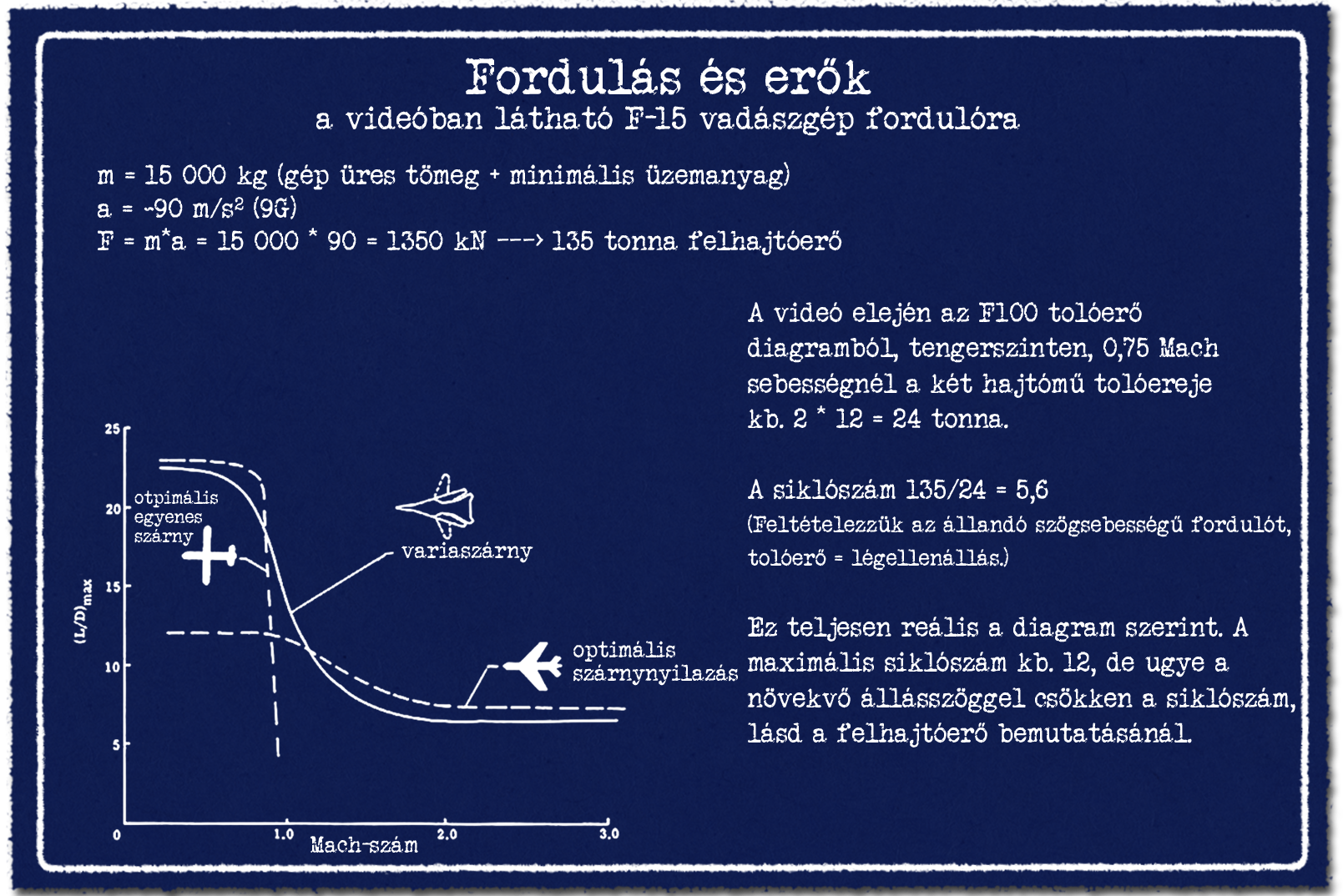
Ennél a pontnál idézzük fel a korábban tanultakat. A felhajtóerő bemutatásánál láttuk, hogy ahogy nő az állászög, úgy nő a felhajtóerő-tényező mellett légellenállás-tényező, tehát a légellenállás is. Na emiatt szükséges a gyors irányváltoztatáshoz hatalmas tolóerő, mert a hatalmas felhajtóerő előállítása brutálisan megnöveli a légellenállást is. Vegyünk példaként egy F-15 vadászgépet, ahogy 0,7-0,8 Mach sebesség táján végrehajt egy nagyjából 9G túlterhelésű fordulót. A gép tömege kb. 15 tonna, mert kevés üzemanyaggal repülnek ilyenkor. Tehát ennek legalább a kilenceresét állítja elő felajtóerőben a gép a fordulóban, nagyjából 135 tonnát. A tolóerő bemutatásánál használt görbét előszedve tudjuk, hogy egy hajtómű tolóereje ekkor kb. 12 tonna, kettőé akkor 24 tonna. Tehát a siklószám kb. 135/24, ez 5,6. Ez teljesen reális. A felhajtóerőt bemutató diagramon láttuk, hogy nagy állásszögeknél a légellenállás növekedése miatt romlik a siklószám. Vízszintes repülésben kisebb állászög mellett a siklószám lehet akár 10 felett is.

A repülőgép pályája és erők

Hogyan értelmezzük a nehézségi gyorsulást? Ehhez szükséges megismerkedni a forduló szögsebesség és a fordulósugár fogalmakkal. Egy körpályán haladó tömegpontnak gyorsulása van, ha egyenletes szögsebességgel halad egy középpont körül. A leegyszerűbb példa, amikor egy tömeget pörget valaki egy kötél végén. A kötélen ébredő erő a nehézségi gyorsulásból származik. Ez amiatt van, mert a sebesség az vektormennyiség és nem skalármennyiség. A sebesség változása az a sebességvektor irányának a megváltoztatását jelenti a körpálya irányára merőlegesen, minden időpillanatban. Attól, hogy maga a vektor hossza, tehát a skalárisan értelmezett sebesség állandó, attól még gyorsulás történik, ezt hívjuk centripetális gyorsulásnak. A gyorsulás a képen látható összefüggéssel számolható.

A körpályán, állandó sebességgel haladó testre ható gyorsulást nevezzük centripetális gyorsulásnak. A centripetális erő négyzetesen arányos a sebességgel, fordítottan a sugárral és egyenesen arányos a repülőgép tömegével. A centripetális gyorsulásból eredő túlterhelést „G-erőkként” szokták hívni, ez egy viszonyszám, ami megmutatja, hogy a normál gravitációs gyorsuláshoz képes a repülőgépet és a pilótát hányszor nagyobb erő, vagyis gyorsulás terheli. A gravitációs gyorsulási együttható 9,81 m/s², am jó közelítéssel 10. Tehát egy 5G-s fordulót végrehajtó repülőgép centripetális gyorsulása kb. 50 m/s².

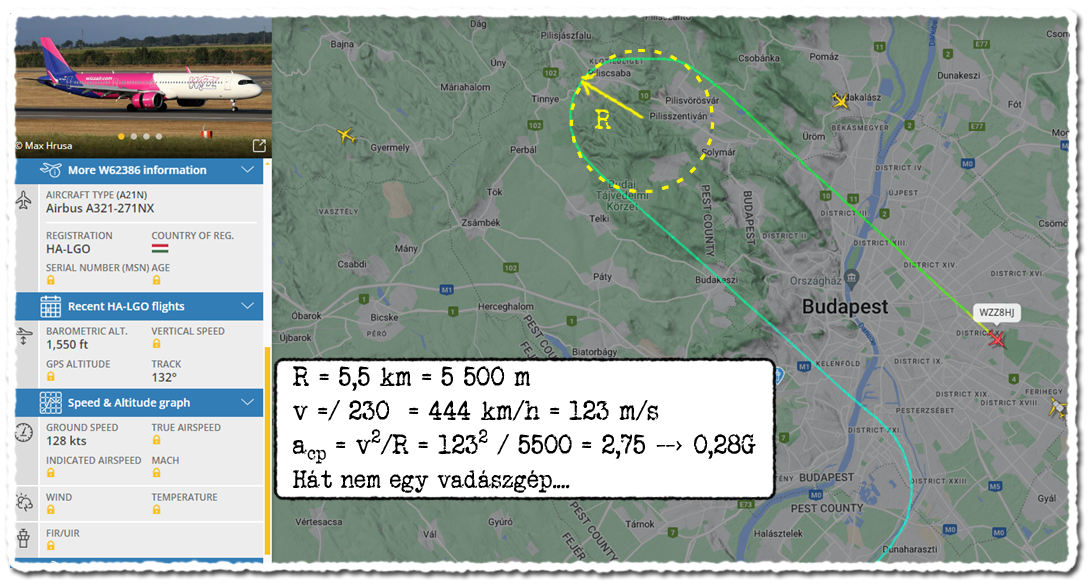
De, hogy lássuk a különbséget számokban egy vadászgép és egy utasszállítógép között. A példaként használt F-15-nél 0,7 Mach vagyis kb. 238 m/s sebességnél 650 méteres fordulósugár mellett jön ki a 9G túlterhelés. Mi az, amit az átlagember megtapasztal egy kereskedelmi utasszállítón? A képen látható pályán a felső fordulónál a sebesség átlagosan 230 csomó volt, ami 444 km/h, vagyis 123 m/s. A forduló sugara Pilisvörösvár és Telki közötti távolságnak kb. a fele, ami nagyjából 5,5 kilométer. Az ebből számolható túlterhelés 0,28G. Ezt már érzi az ember utazás közben, de látható, hogy a vadászgépek manőverező légiharcban teljesen más ligában fociznak. A túlterhelés mértéke fej-láb irányú erőt jelent. Érdekesség amúgy, hogy az átlagember autózás közben nagyjából ugyanekkora mértékű oldalirányú gyorsulást érez még komfortosnak. Az meg már csak tényleg a margóra, hogy a Forma 1-es versenyzők akár 5G túlterhelést is kapnak oldalirányban a nagysebességű kanyarokban.

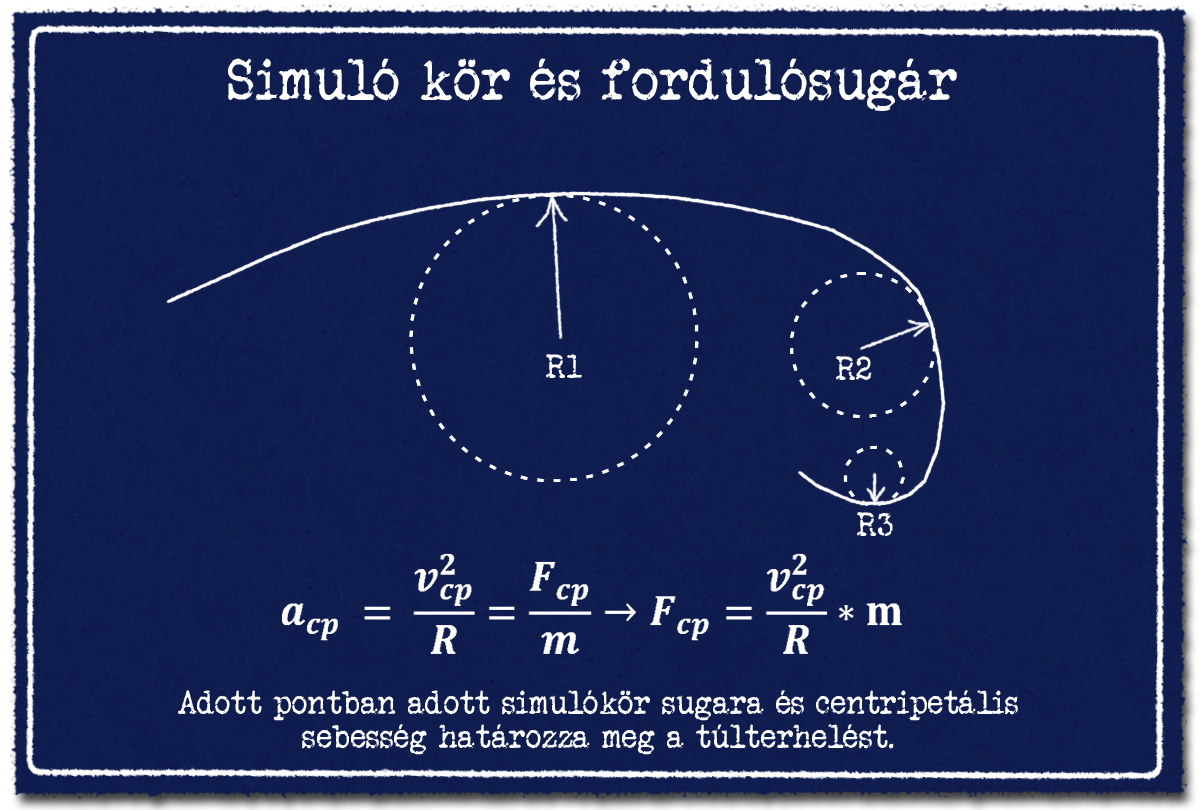
Mi a probléma a modellel? Egy repülőgép vagy rakéta ritkán repül tökéletes körpályán és állandó kerületi szögsebességgel. Amennyiben felrajzoljuk egy légiharc-rakéta vagy repülőgép által lerepült pályát manőverezés közben, akkor látható, hogy még, ha nem is körpályáról van szó, de olyan, mintha változó sugarú körívek alkotnák azt. Matematikai nyelven a pályának az adott pontban érvényes görbülete, adott pontokban meghatározható simulókörök sugarával írható le.[12] Ezek sugara adja meg nem körpálya esetén az adott pontban érvényes görbületi sugarat, amivel használható a fent bemutatott összefüggés a gyorsulásokra állandó centripetális sebesség esetén. A centripetális gyorsulás vektor a fordulósugár közepe felé mutat.

Az ábrán egy elképzelt forduló manőver és annak pályája látható. Ez adódhat úgy, hogy állandó sebesség mellett egyre nagyobb túlterhelésű fordulót hajt végre a repülőgép. De az is lehetséges, hogy folyamatos sebességvesztés mellett a forduló szögsebesség csökken, de a kisebb sebesség mellett mégis kisebb fordulósugár adódik ki. Tehát repülőgép lassabban fordul, de mégis szűkebben, kisebb sugáron.

Mi következik a fentiekből? Ha állandó szögsebességgel fordul a repülőgép az Y tengely körül, és ennek forduló szögsebessége azonos, tömegpont simuló körének körpályán értelmezett forduló szögsebességével, akkor az állásszög állandó. A repülőgép pont annyit fordul el a tengelye körül, amennyit a sebességvektora is. Ha a gép előrehaladási sebessége sem változik, akkor állandó túlterhelésű fordulóról beszélünk.

Ebből viszont ismételten az következik, hogy az elemi tömegpont modell nem írja le, hogy egyenes vonalú repülés és a fordulás közötti átmeneti időszakban mi történik. A kis magasságú bemutató repüléseken jól látszik, hogy a gép markáns irányváltozása mindig annak állásszögének változását követi le. Ahogy repülőgép elfordul a saját tengelye körül és növekszik az állásszög, úgy ébred egyre nagyobb felhajtóerő, ami aztán megváltoztatja a sebességvektor irányát. Amikor a sebességvektor megváltozásának sebessége azonos azzal, amennyivel a repülőgép a bólintási szöge változik, akkor állandó szögsebességű fordulóról beszélünk.

A Kobra manőver[13] során a repülőgép haladási irányi és bólintási szöge jelentősen eltér.

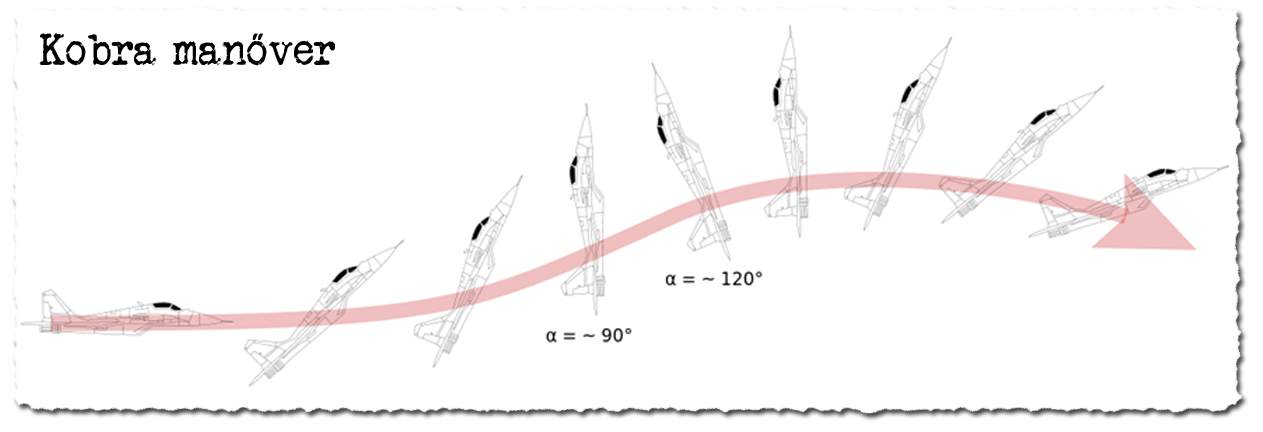
A fentiek következménye az, hogy lehetséges a repülőgépet gyorsabban forgatni például bólintási szög körül, mint amekkora a sebesség vektor forduló szögsebessége. Ennek eredménye például a Kobra manőver, amikor repülőgép haladási irányához képes extrém nagy állásszöggel haladhat, rövid ideg akár 90-120 fokot is elérheti az állásszög. Ez nem tartós üzemi tartomány, ez csak tranziens állásszög.

A vadászgépek extrém nagy túlterhelésű és állásszögű fordulóban túlléphetik a tartósan engedélyezett állásszöget. Az ilyen fordulókban olyan mértékű légellenállást produkálnak, hogy gép nagymértékben lassul, nincs az hajtómű teljesítmény, ami ezt kompenzálni lenne képes.

Amikor a felhajtóerő és a haladási irány által bezárt szög tartósan nagyobb az állásszögnél, az nagyon nem kívánatos eset, ez már a nem irányítottrepülés tartománya. Egy ilyen látható a bevágott videó részleten. Az F-16 még alapvetően arra repült, amerre az egyenes repülés során haladt, de az aszimmetrikus fegyverzet konfiguráció és gyors állásszög változtatás miatt olyan keresztiárnyú légerők és nyomatékok ébredtek, amik a gépet több tengely körül is forgatták. A repülőgép ettől számottevően lassult, de a sebességvektora lényegében az előrehaladási irány körül oszcillált, ameddig egy fordulóval a végén újra irányított repülést értek el.

Na, ezzel nagyjából képbe kerültünk, hogy hogyan repül egy vadászgép és milyen fő tényezők befolyásolják a teljesítmény paramétereit, a következő epizódban számszerű példákon keresztül történik a teljesítmény bemutatása.

 https://eaglepubs.erau.edu/introductiontoaerospaceflightvehicles/chapter/performance-envelopes/

 [1] https://youtu.be/J3rvFElP8z8?t=518

[2] https://www.youtube.com/watch?v=YMfUP8lx0FU

[3] https://www.grc.nasa.gov/www/k-12/airplane/machang.html

[4] https://eaglepubs.erau.edu/introductiontoaerospaceflightvehicles/chapter/flying-fast/

[5] https://youtu.be/gJxi-NYbPWU

[6] https://youtu.be/X8CpNCm6O50

[7] https://aviation.stackexchange.com/questions/68320/how-can-an-f-22-raptor-reach-supersonic-speeds-without-having-supersonic-inlets

[8] https://youtu.be/HekbC6Pl4_Y

https://www.twz.com/shockwaves-bend-light-around-transonic-f-35c-in-spectacular-images

[9] https://www.grc.nasa.gov/www/k-12/UEET/StudentSite/dynamicsofflight.html

http://ze-engineer.blogspot.hu/2010/06/airplane-control-surfaces.html

[10] A „flap” hidraulikus munkahengerekkel működtetett, a „slat” az aerodinamikai erők hatására „esik” ki magától a szárnyból vagy nyomódik vissza a helyére a légerők által, a Me-109 vadászgépek volt ilyen. Nagysebességű vadászgépeken csak hidraulikus munkahengerekkel mozgatott orrsegédszárnyt használnak.

[11] Newton II. törvénye. F =m*a. Newton valójában nem ebben a formában fogalmazta meg ez az összefüggést, de számtalan esetben ez a forma célszerű és használható.

[12] https://hu.wikipedia.org/wiki/G%C3%B6rb%C3%BClet https://goo.gl/55bSy9

 Közreműködők

• Molnár Balázs                                Grafika, animáció, szöveg
• Hpasp                                             Technikai lektor
• Cifka”Cifu” Miklós                           Technikai lektor
• Farkas Gábor                                  Technikai lektor

 A Patreon és Donably felületek elérhetősége az extra tartalomhoz és támogatásához.

https://www.patreon.com/militavia

https://www.donably.com/militavia-katonai-repules-legvedelem