Előszó

Az első részben megismerkedhettünk a vadászgépek teljesítményét befolyásoló fő tényezőkkel, illetve, hogy mozgásuk és rájuk ható erők jó közelítéssel hogyan írhatók le. Ezek után következzen teljesítményük konkrét számokkal, néhány típussal bemutatva, leszámolva sztereotip kijelentéssekkel és legendákkal, ami egyes vadászgépekről vagy úgy általánosságban kering a köztudatban.

Teljesítmény számokban

Csúcssebesség

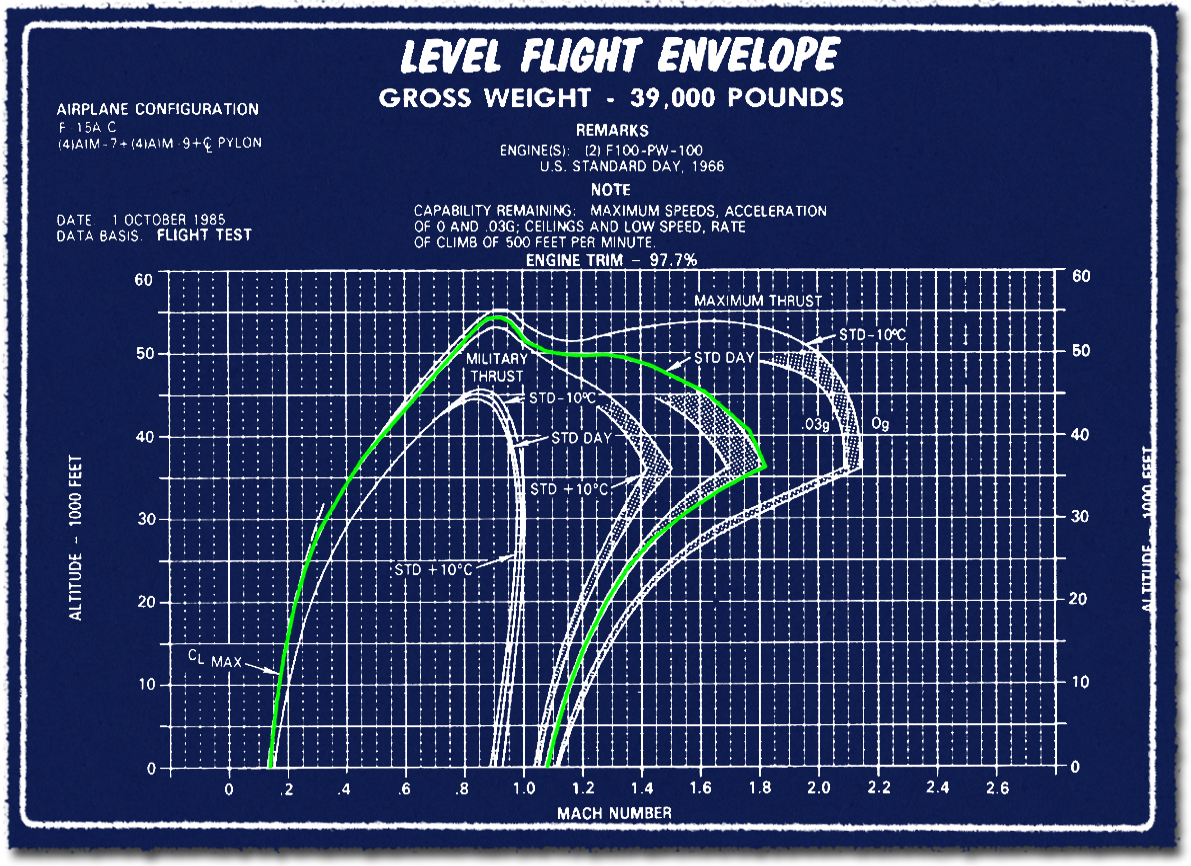
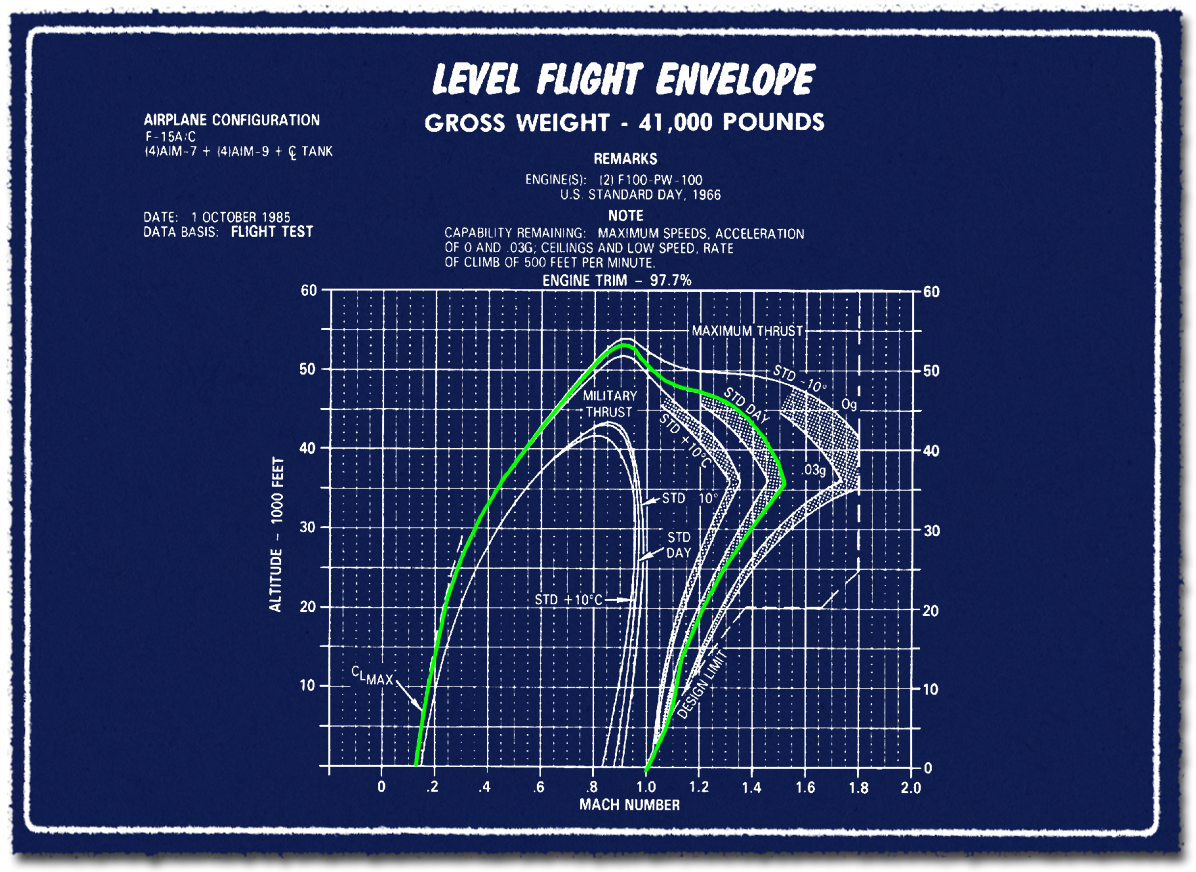
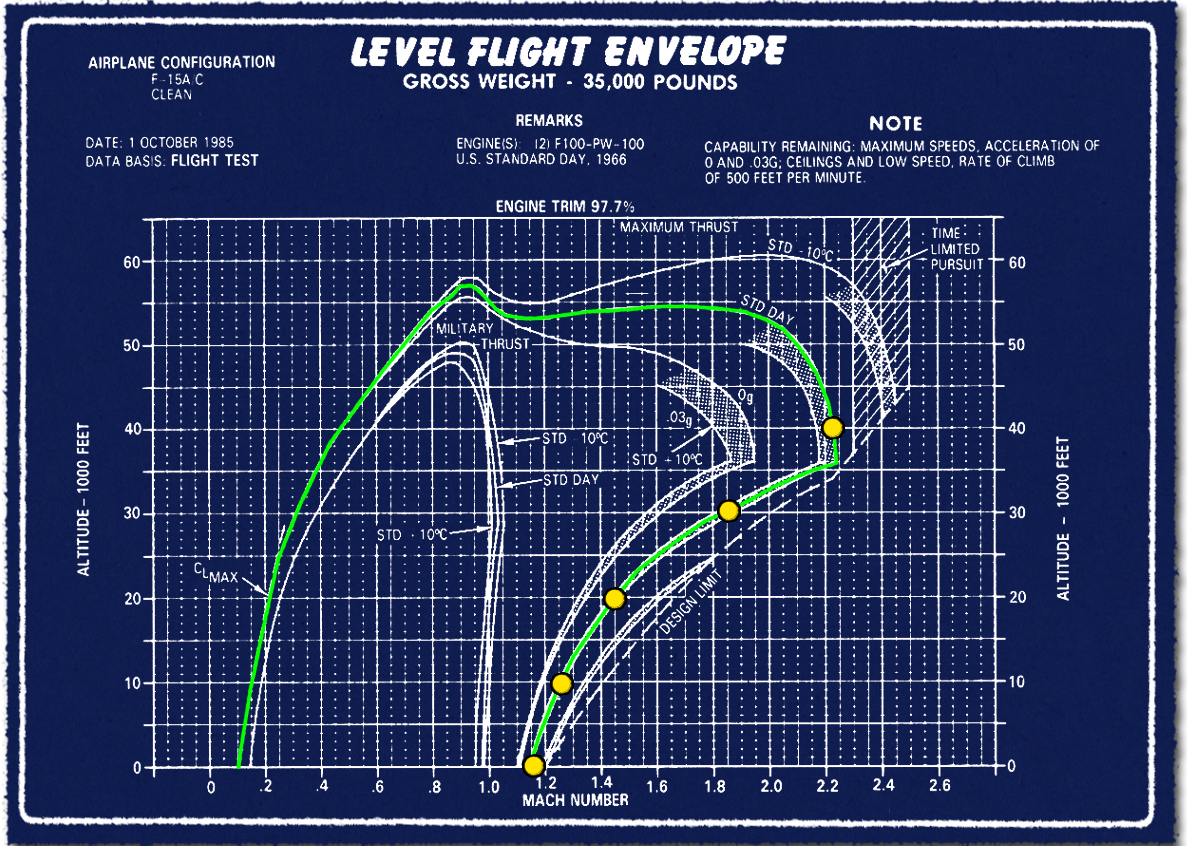
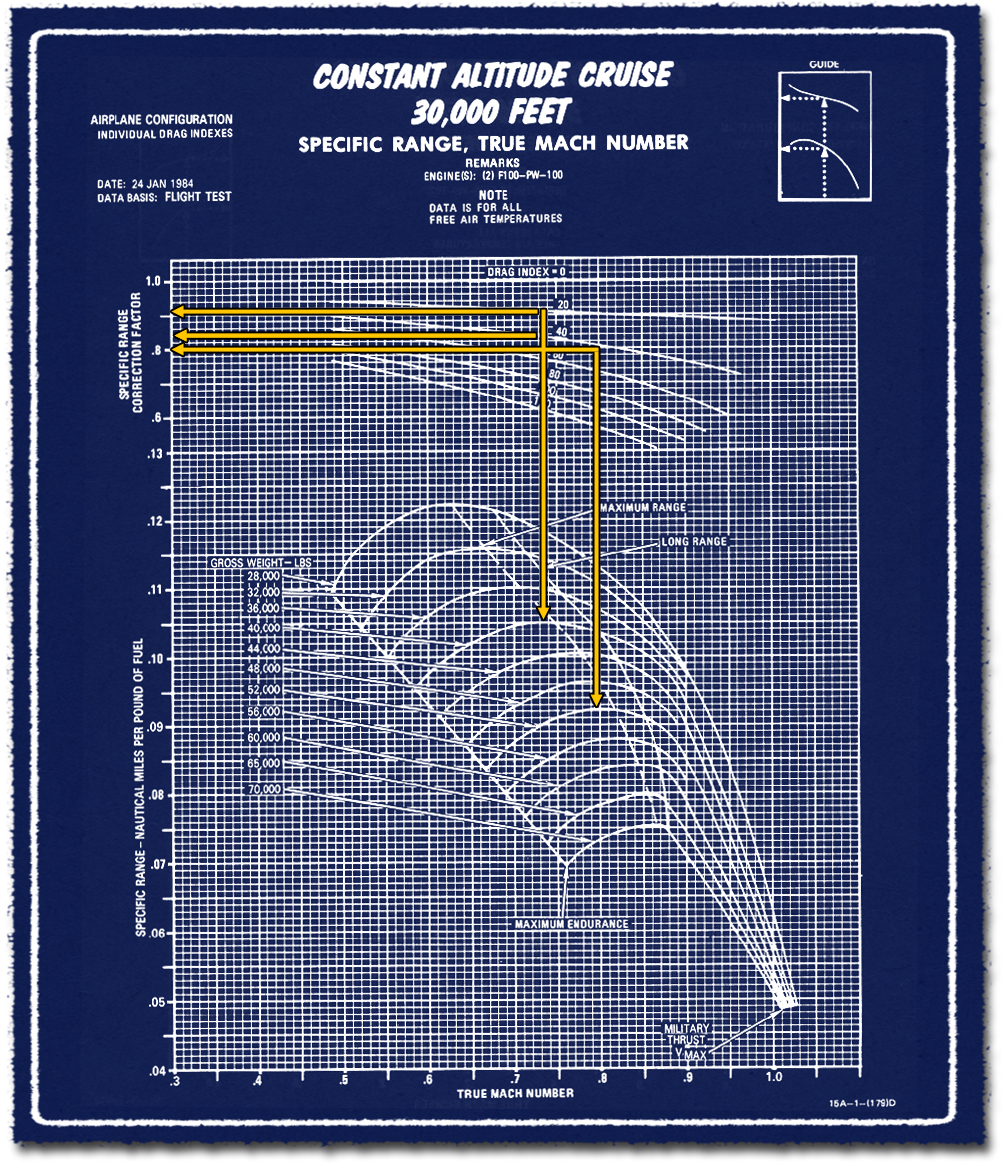
Első lépésben tegyük tisztába, hogy mekkora az elméleti és gyakorlati csúcssebessége a vadászgépeknek. Ehhez kezdésnek három diagramot használok fel, amin az F-15A vadászgép csúcssebessége és minimális sebessége látható, három eltérő konfigurációban sztenderd légkör esetén. Foglalkozzunk most csak a csúcssebességgel. A három diagramon majd a függesztmény nélküli, 4+4 darab Sparrow és Sidewinder légiharc rakétával, illetve 4+4 darab rakéta és a törzs alatti póttartállyal elérhető maximális és minimális sebességet mutatja, 35, 39 és 41 ezer font, vagyis kb. 16, 17,5 és 18,5 tonnás tömeggel. Kezdjük az elsővel.

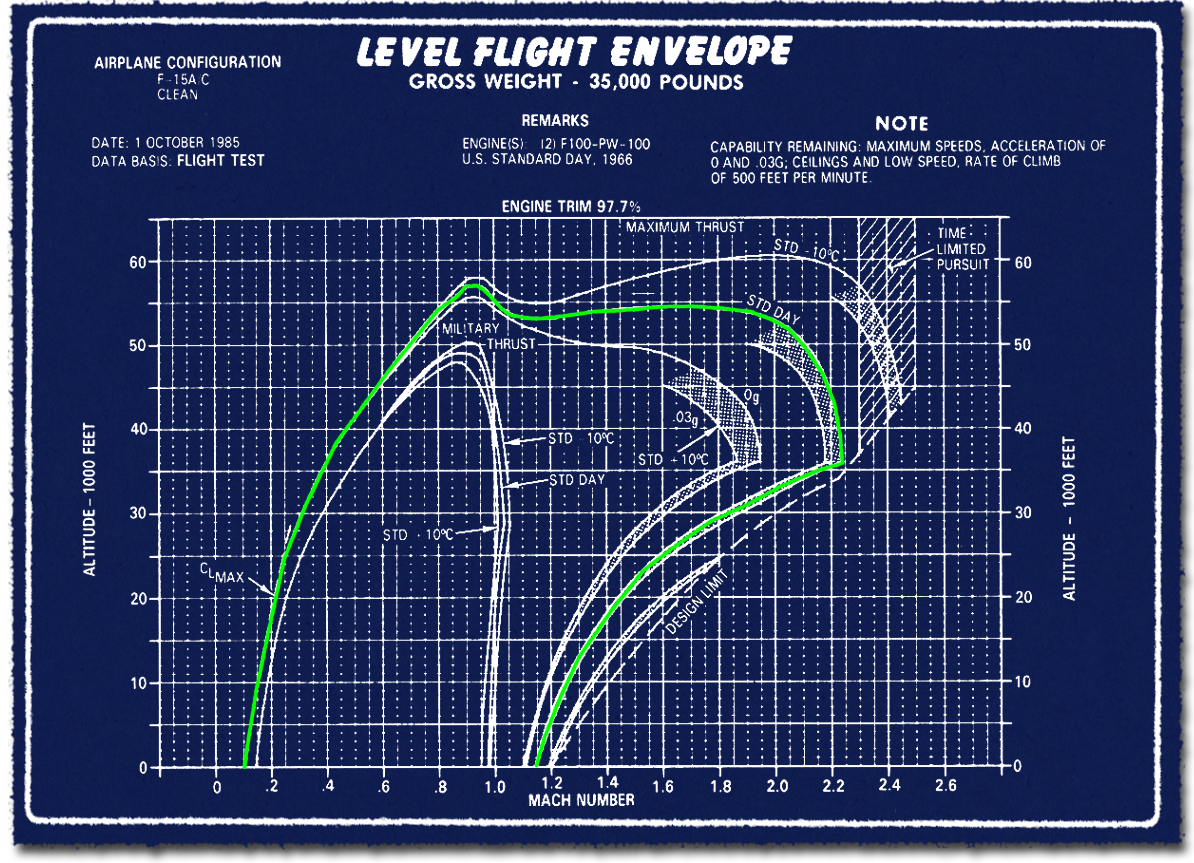
• Fegyverzet nélkül a csúcssebesség 36 ezer láb, vagyis kb. 11 kilométer magasan kicsivel 2,2 Mach felett van. Az F-15 a sokszor és sok helyen tévesen hivatkozott 2,4 Mach csúcssebességét valójában csak hideg időben képes elérni, vagy legfeljebb az élettartam kárára megnövelt tolóerővel, lejtőn és hátszélben. A csatornán taglalt F-15EX változat, a marketing és fogalmatlanok által agyon hangsúlyozott 2,5 Mach sebességet szintén nem képes elérni, hiába rendelkezik az erősebb F110-GE-129 hajtóművel. A nagyobb, két személyes kabin miatt a gép légellenállása számottevően nagyobb. Na nem mintha lenne bármi jelentősége ennek...
• 4+4 darab Sidewinder és Sparrow légiharc-rakétával az elérhető csúcssebesség kb. 1,8 Mach-ra csökken. Az elméleti csúcssebesség már a 8 darab, relatíve kisméretű légiharc rakéta hordozásakor is számottevően kisebb. Ennek oka, hogy kis méretük és homlokfelületük ellenére nagymértékben rontják a hullámellenállást.
• És végül az utolsó diagramon, a 4+4 darab rakéta és egy törzs alatti póttartállyal már csak 1,5 Mach az elérhető elméleti csúcssebesség.

Figyelem, a diagramok az elméleti csúcssebességet mutatják meg, arról semmiféle információt nem adnak, hogy annak elérése mennyi ideig tart, mekkora gyorsításai úthossz szükséges, illetve hogy mennyi üzemanyag szükséges ahhoz. Tehát nem derül ki, hogy milyen áron érhetők el azok. A harcászatilag kihasználható csúcssebességek messze ezen értékek alatt vannak, ahogy majd később látni fogjuk.

Egy rövid megjegyzés még így az elején. Adott célra, adott diagram használata célszerű, adott paraméterek állandónak tekintése mellett. A csúcssebesség vizsgálatánál lényegében a magasság változását ábrázoljuk eltérő tömeg és fegyverzettel. Amikor más paraméter vizsgálata a cél, akkor másfajta diagram használata célravezető. A diagramok egy referencia állapotot mutatnak, az ettől való kis eltéréseket egy idő után érzi az ember, lehet interpolációt alkalmazni, de ezek kompenzálására maguk a diagramok mellé tett utasítások is szolgálnak útmutatással.

A diagram tartalma a laikusok számára furcsa lehet. Az első részben láthattuk, hogy hajtóművek tolóereje, tehát a teljesítménye csökken, ahogy nő a repülési magasság. Akkor hogyan lehet, hogy a csúcssebesség kb. 36 ezer láb, vagyis 11 ezer méter magasan van, amikor a tolóerő sokkal kisebb, mint tengerszinten? Hát úgy, hogy a tolóerőhöz képest a levegő sűrűségének csökkenése sokkal jobban befolyásolja a csúcssebességet, mint a kisebb tolóerő. Még kisebb tolóerővel is nagyobb csúcssebesség érhető el, mint kis és közepes magasságban. Nincs itt ellentmondás? Nincs. A kutya ugyanis az eltérő gyorsulásoknál van elásva. Térjünk hát át erre a témára, ahol továbbra is az F-15A-t vizsgáljuk.

Gyorsulás

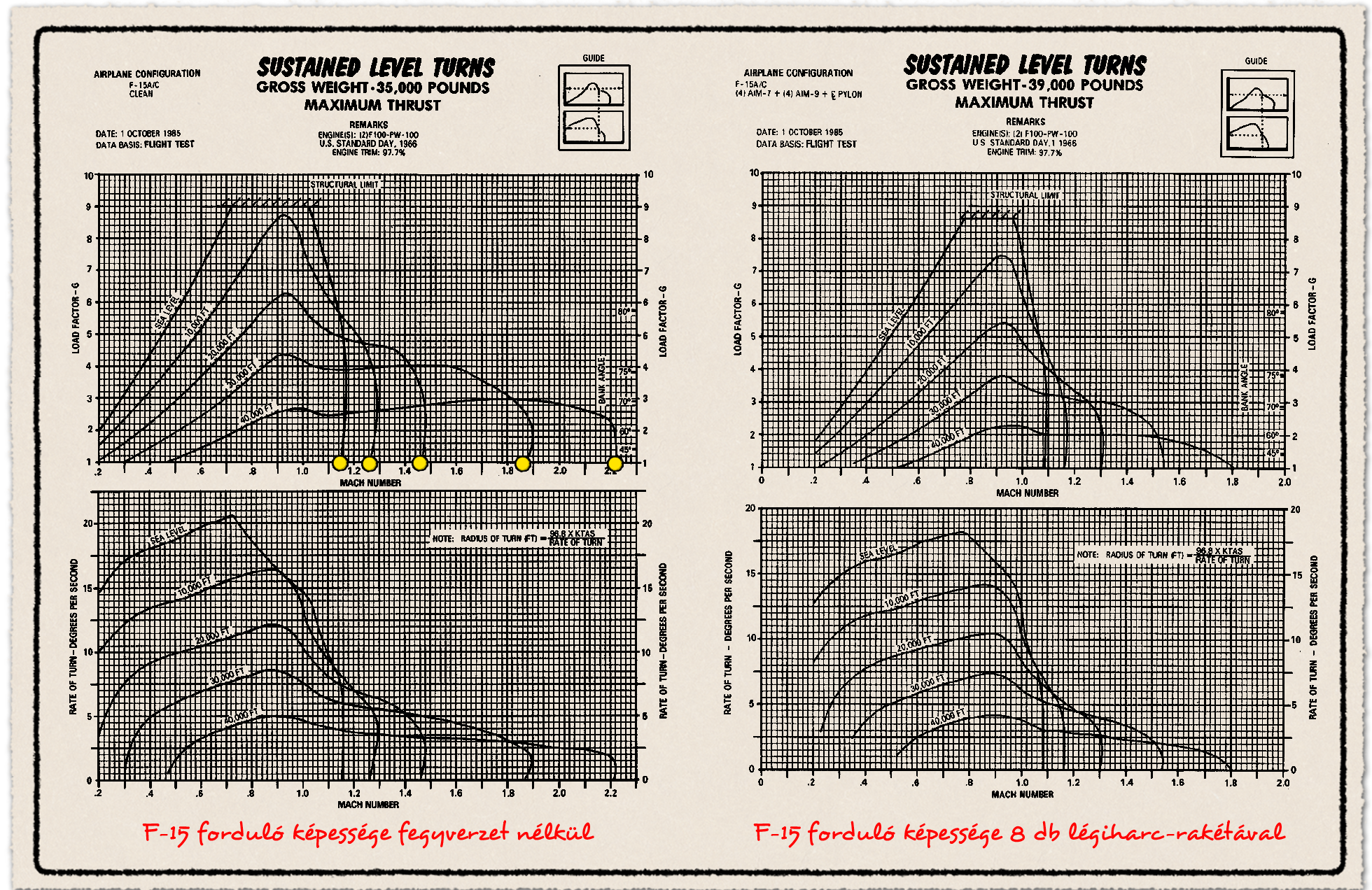
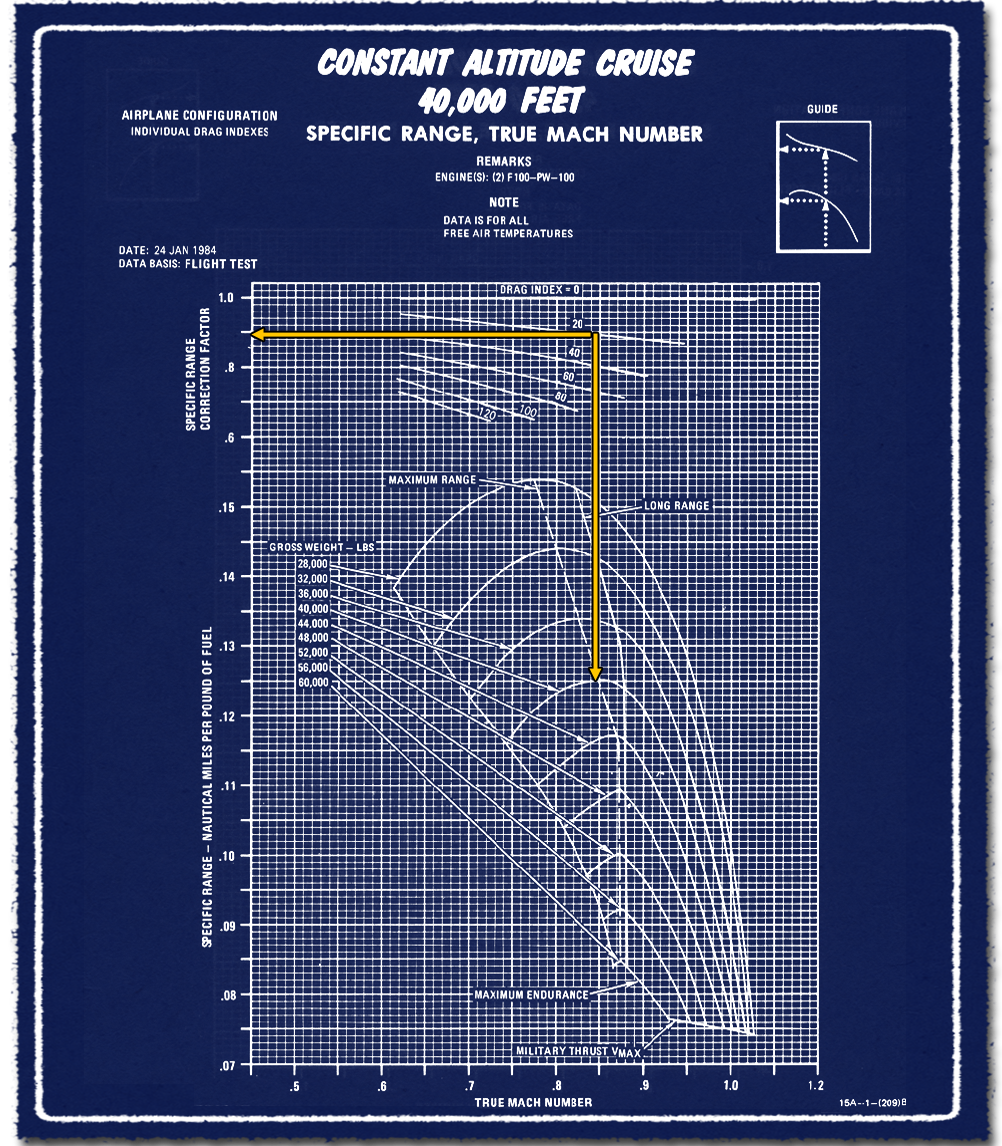
A gyorsulás bemutatásához szintén három darab diagram szükséges, ezeken 40 ezer láb, vagyis kb. 12 kilométer magasságban elérhető gyorsulások láthatók a három vizsgált konfigurációban, 0,8 Mach sebességről.

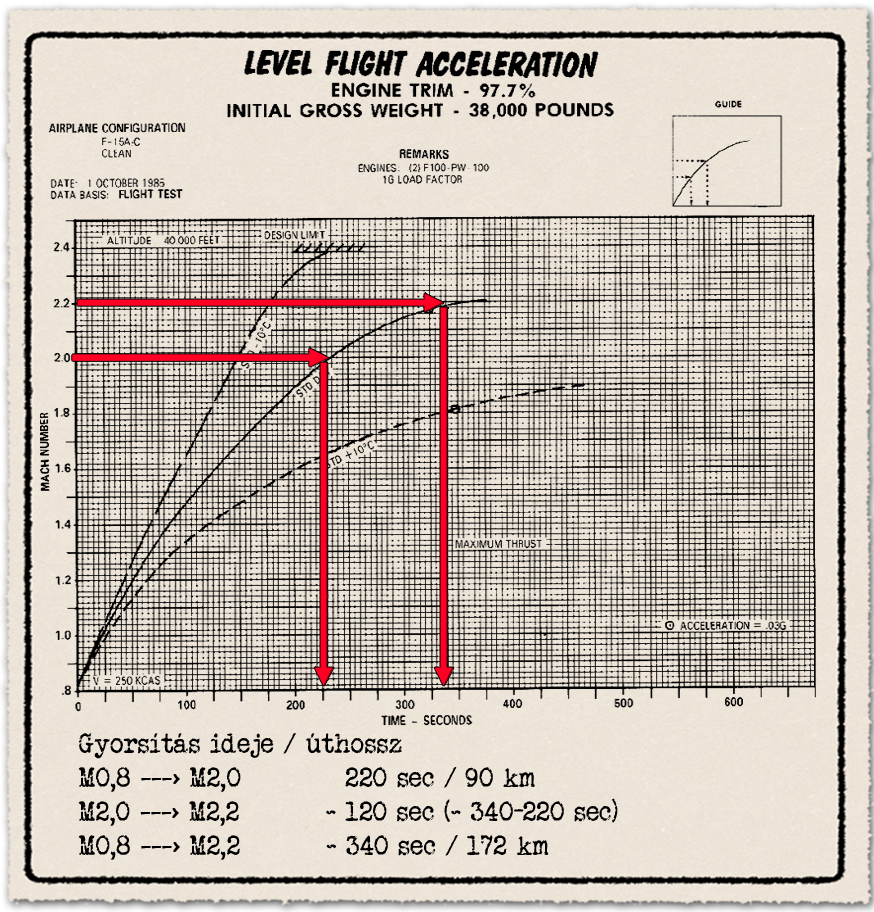
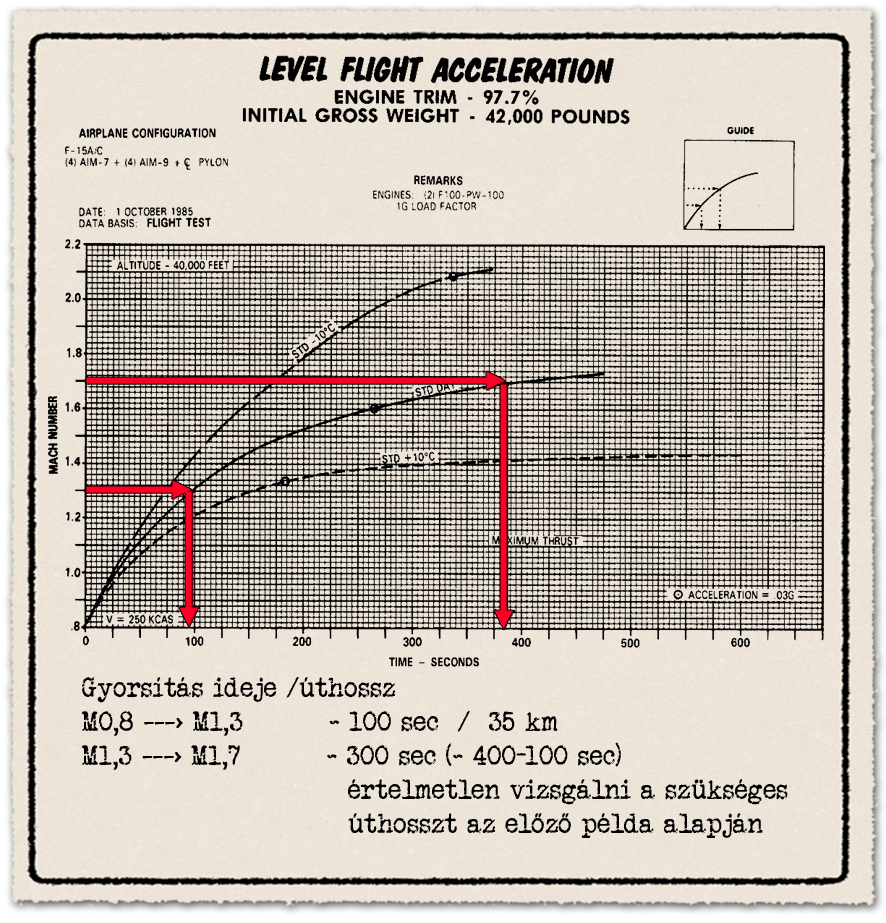
• A fegyverzet nélküli géppel szubszonikus őrjárati sebességről, 0,8 Mach-ról 2 Mach-ra 220 másodpercig, 2,2 Mach csúcssebességre 340 másodperc, vagyis majdnem 6 percig (!) tart felgyorsítani. Már ez is jól mutatja, hogy az elméleti csúcssebesség diagram értékei mennyire elméletiek. A csúcssebesség közelében a gyorsulás borzalmasan alacsony. A 2 Mach sebességről 2,2 Mach-ra gyorsítás ideje összemérhető a 0,8-ről a 2,0 Mach sebességre gyorsulással. Ez nagyjából mutatja, hogy mennyire komolyan vehető egy vadászgép elméleti csúcssebessége.

A csúcssebesség eléréséhez 1,6 Mach becsült átlagsebességgel 172 kilométerre van szüksége az F-15-nek, kb. 38 000 font, vagyis kb. 17 tonna átlagos tömeggel. Még a 2 Mach sebesség elérése is kicsivel több, mint 90 kilométert vesz igénybe. Szerintem elsőre is látszik, hogy harcászatilag értelmezhetetlenül nagy távolság mindkét érték. Ráadásul a gép fegyvertelen, fegyverzettel repülve ennél is rosszabb a helyzet.

• 4+4 darab légiharc rakétával az 1,7 Mach elérése majdnem 400 másodpercig tartana, több, mint 6 percig. Megint jól látszik, hogy az elméleti csúcssebességnek lényegében semmi köze a harcászatilag kihasználhatóhoz. Az 1,3 Mach sebességet kb. 100 másodperc alatt éri el a gép, ami kb. 35 kilométer vesz igénybe, nagyjából 1,1 Mach átlagsebességgel. Ez még reális vadászgépek közötti összecsapásnál, illetve más esetben is, ha szükség lenne huzamosabb ideig ekkora sebességgel repülni. Közelítünk a realitásokhoz és látszik, hogy a kontraszt mennyire éles az 2,2 Mach elméleti csúcssebességhez képest.
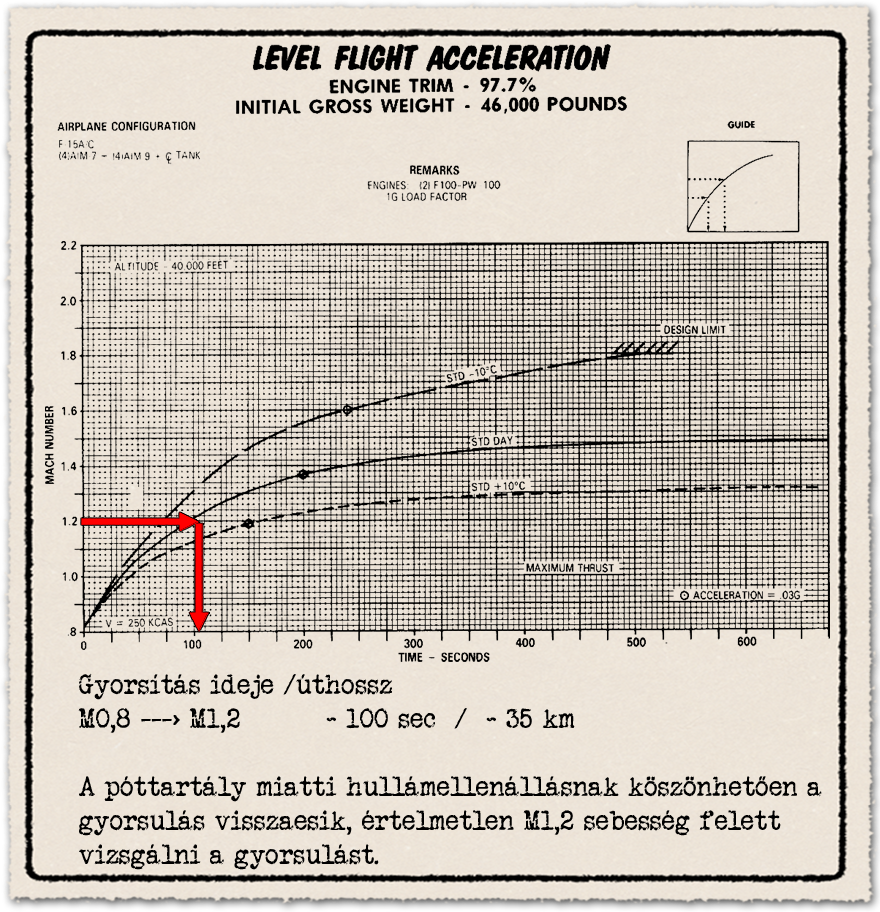
• 4+4 darab légiharc-rakéta és póttartály esetén érdekes módon a gyorsulás 1,2 Mach sebességig viszonylag közel marad a póttartály nélküli esethez. Póttartállyal 100 másodperc, anélkül 80 másodperc alatt éri el azt az F-15A. Ez a Mach számmal változó hullámellenállásból adódik. A póttartály csak 1,2 Mach felett rontja le brutálisan a gyorsulást.

Az a számokból világosan látszik, hogy a harcászatilag értelmezhető csúcssebessége az F-15-nek 4+4 darab légiharc rakétával nagyjából 1,3 Mach táján volt a hidegháború alatt, extrém hideg és egyéb speciális feltételek teljesülésekor esetleg 1,4 Mach. Ma, a AIM-7 Sparrowhoz képest kisebb átmérőjű AIM-120 AMRAAM rakétával ez talán 0,1 Mach értékkel magasabb, de kb. itt ér véget a történet. Vadászgépek közötti harc esetén ennél nagyobb sebességre gyorsítani gyakorlatilag nem lehetséges. A lokátorok észlelési távolsága, illetve a nagy magasságban az AIM-120 és hozzá hasonló légiharc-rakéták indítási zónája akkora, ami nem tesz lehetővé 30-40 kilométernél hosszabb gyorsítási szakaszt, főleg, ha még az ellenséges vadászgép is hasonló manőverbe kezd.

A vizsgált modell ráadásul azzal számol, hogy az F-15 vadászgép 9-10 kilométeres magasságban és 0,8 Mach kezdősebességgel kezdi meg a gyorsítást. Ha példaként használt vadászgép lassabban és alacsonyabban repül, akkor a gyorsuláshoz szükséges táv és idő a bemutatottnál is hosszabb, hiszen még fel is kéne emelkedni előbb. Bár azt hozzá kell tenni, hogy 40 ezer láb helyett inkább csak a 30-35 ezer láb tartományba emelkedés a célszerű. Az elméleti csúcssebesség itt kisebb, de azt ugye úgysem akarja elérni senki. Ezért cserébe a gyorsulás picit jobb, mint a diagramokból leolvasható értékek 40 ezer láb magasságban. Az 1,3-1,4 Mach gyorsabban elérhető, kicsit magasabb lesz így a fogyasztás, de az eltérés nem jelentős, megéri a jobb gyorsulásért cserébe.

Az F-15 teljesítménye jól mutatja a többi hagyományos vadászgép korlátait is. Minden többfeladatú vadászgép, ami külső függesztéssel hordozza a fegyverzetet jellegre pontosan ugyanúgy viselkedik. Ettől komoly eltérés nem lehetséges, mert a fizika tudja a dolgát. A nagyotmondó PR szlogenek és a propaganda a repülőgépek légellenállását nem tünteti el. Főleg úgy, sok mai vadászgép a 40 évvel ezelőtti elődök alapformájával bír, lásd F-15EX és Szu-35 példáját.

Típustól és fegyverzettől függően legfeljebb az arányok tolódnak el 0,1-0,2 Mach értékkel ettől a viszonyítási ponttól. Egy deltaszárnyú Eurofigther Typhoon, annak félgenerációs ugrást jelentő hajtóművével a ’70-es és ’80-as évekhez képest, süllyesztve elhelyezett légiharc rakétáival lehet, hogy azonos 1,4 Mach körüli sebességgel
10-15%-kal kisebb fajlagos fogyasztással képes repülni, mint egy F-15 vagy adott esetben az értelmezhető hatósugárhoz tartozó kihasználható csúcssebessége picit magasabb. Vagy fordítva, egy erőtlenebb és kisebb vadászgép, mint például a Gripen még ennyire sem képes, vagy a királykategóriától kicsit elmaradó F-18 Hornet és Super Hornet sem.

Visszatérve az elásott kutyára a csúcssebesség és a gyorsulások közötti látszólagos ellentmondásra, lássuk a gyorsulást kismagasságon is. A 40 ezer helyett 10 ezer lábon, vagyis kb. 3 kilométer magasan elérhető gyorsulás látványosan mutatja, hogy a fizika hogyan teszi a dolgát. 40 ezer lábon 0,8-ról 1,4 Mach sebesség elérése, függesztmény nélkül 80 másodpercet vett igénybe. Ezt lehet számszakilag is nézni, hogy 0,6 Mach-ot gyorsult az F-15 vagy a két sebesség arányát is, hogy 75%-kal lett gyorsabb. Ebből az adódik, hogy a mozgási energia nagyjából háromszorosára nőtt, ami a sebesség négyzetével arányos. Ebben a sebesség tartományban még majdnem lineáris gyorsulás.

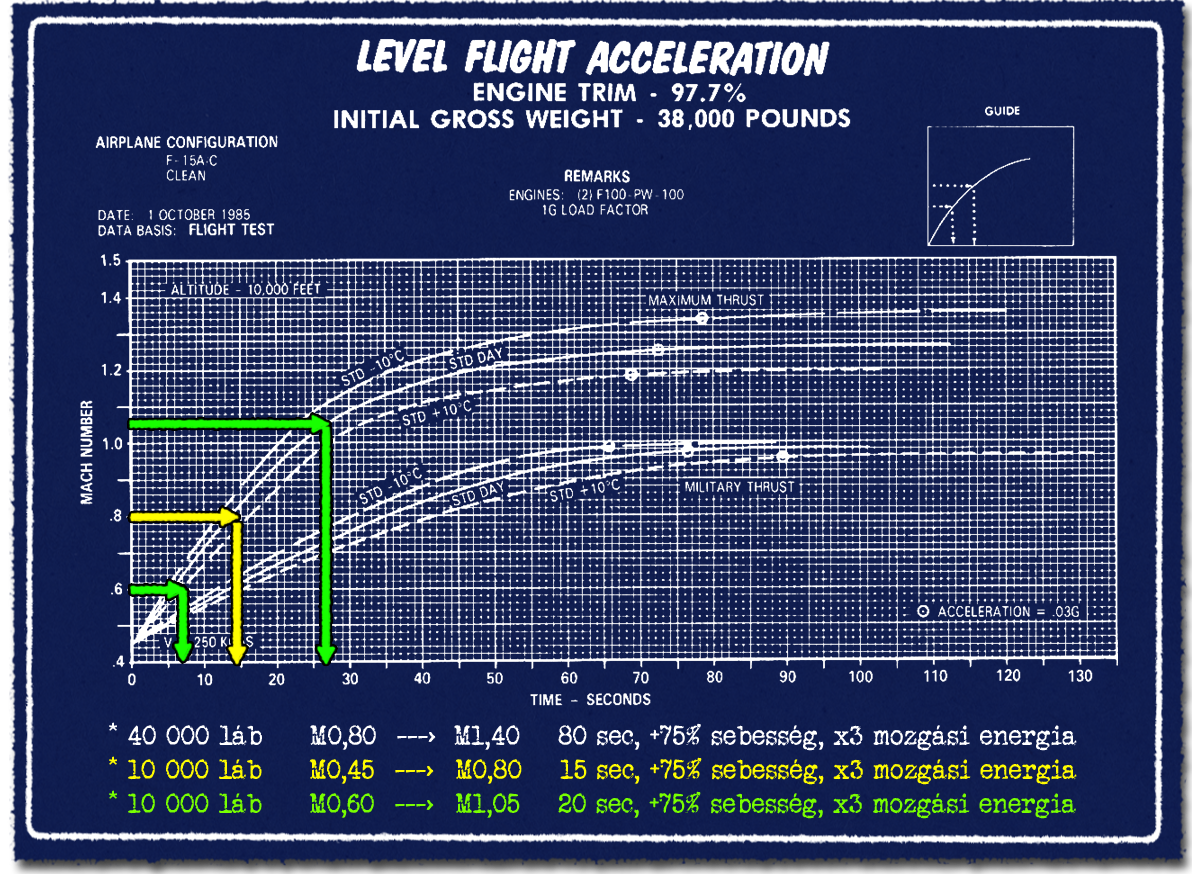
Mi a helyzet 3 kilométer magasan? Nagyjából 0,4 és 1 Mach között itt is majdnem lineáris a gyorsulás. A plusz 75% sebesség összegyűjtése 0,45 Mach kezdősebesség esetén 0,8 Mach, 0,6 Mach-ról gyorsítva 1,05 Mach-ra adódik. A kisebb kezdősebességről mindössze 15 másodperc alatt, a nagyobb kezdősebességnél is kb. 20 másodperc alatt háromszorozta meg a mozgási energiáját az F-15. Csak 1,1 Mach felett csökken le számottevő mértékben a gyorsulás. Lényegében a 0,4 Machtól 1,15 Mach sebességig gyorsítás tart annyi ideig, kb. 35 másodpercig, mint 1,15-ről kb. 1,27 Mach-ra. Itt is megint jól látszik, hogy az elméleti csúcssebességhez közeledve a gyorsulás borzalmasan visszaesik. Ez magasságtól független jelenség, ami amúgy minden járműre igaz, autóra, hajóra is.

Hiába sokkal nagyobb a hajtómű tolóereje, vagyis teljesítménye 3000 méteren, mint 10 000 méteren, a sűrű légkör miatti nagyobb légellenállás a hangsebesség felett olyan mértékben nő, hogy azzal a hatalmas tolóerő sem tud mit kezdeni. Ráadásul ezen a magasságon alig hangsebesség felett repülni is már eszementen magas üzemanyag fogyasztással párosul, erről majd kicsivel később esik szó.

Összefoglalva, a vadászrepülőgépek csúcssebessége és elérhető maximális gyorsulása teljesen más sebesség és magasság tartományban van. Ezt amúgy majd egy másik diagramon is megmutatom később, ahol talán még szemléletsebben látszik ez jelenség.

Üzemanyag fogyasztás harchelyzetben

Visszatérve a harcászati vetületre. A másik tényező, ami miatt az elméleti csúcssebesség, de akár annak még töredéke sem használható ki gyakorlatban, az üzemanyag fogyasztás. A 4+4 darab AIM-7 és AIM-9 rakétával repülő F-15 percenkénti üzemanyag fogyasztása látható az ábrán levő görbéken. Az értékek az adott sebesség tartásához szükséges fogyasztást mutatják vízszintes repülésben. A gyorsulás 40 ezer láb magasságon volt vizsgálva, ezért a fogyasztást is ezen nézzük első körben. 

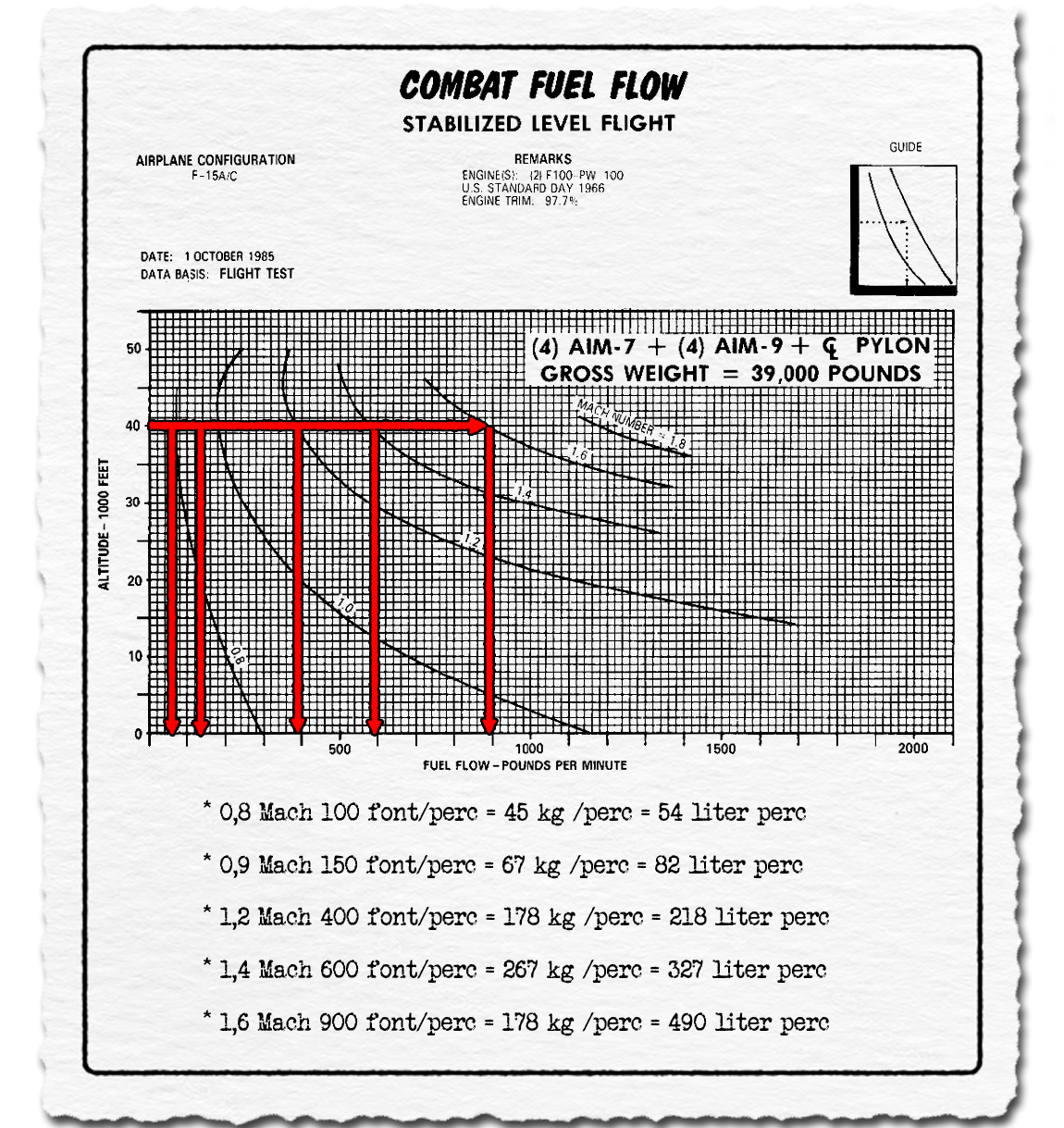
• 0,9 Mach sebességnél, ahol utánégető használata nem szükséges, a fogyasztás percenként kb. 150 font, ami 67 kg, ez kb. 82 liter, hogy érezzük térfogatban is a mennyiséget. Tehát durván 2 font kerozin az 1 liter, ökölszabálynak ez elég is.
• 1,2 Mach sebességnél, amikor már minimális utánégető használata szükséges, 400 font/perc, tehát kb. 2,5-szeres az időegység alatti fogyasztás, mint ami 0,9 Mach sebességnél.
• 1,4 Mach sebességnél a fogyasztás 600 font/perc, ami a 0,9 Mach sebességhez képest négyszeres, a M0,8 gazdaságos utazósebességhez képest már hatszoros.
• 1,6 Mach sebességnél 900 font/perc a fogyasztás, ez az utazósebességhez képest már tízszeres fogyasztás percenként.

Hogy kontextusba helyezzük ezeket fogyasztási értékeket. Az F-15A teljes belső üzemanyag kapacitása kb. 11 500 font, az F-15C-é 13 500 font. Az F-15C belső kapacitása pont annyi, mint amit 15 perc repülés 1,6 Mach sebességet tartva igényelne. Csak ugye a gyorsítás maximál utánégető teljesítménnyel történik, majd utána tartja a sebességet a vadászgép, no meg vissza is kéne repülni a támaszpontra a száguldozás után. Ezeken felül számolni kell még biztonsági tartalékkal és a tartályokból ki nem fogyasztható mennyiséggel is. Nagyon megengedően talán a teljes belső üzemanyag mennyiség 1/3-a az, amivel lehet számolni a gyorsítás és a sebesség tartására.

A fentieket számításba véve, nagy magasságban, 1,6 Mach sebességgel az F-15C nem képes 5 percnél többet repülni és annak is drámai hatása van a hatósugárra egy végig szubszonikus sebességű bevetéshez képest. És még ez is úgy adódik ki, hogy teljesen idealizált az eset. Pontosan a gyorsítás előtt dobja el a póttartályokat a vadászgép a szükséges magasságon. Na meg póttartály sem a fán terem, abból sincs végtelen mennyiség, tehát nem lehet mindig csak úgy ledobni azokat, ha éppen szükségét érzi a száguldásnak a pilóta...

Mit jelent ez a hatósugár csökkenésre lefordítva? 1 perc 1,6 Mach sebességű száguldás a rakétákkal tízszer több üzemanyagot fogyaszt, mint az utazósebességgel repülés. Az 1,6 Mach az utazósebesség duplája. Tehát távolságra fajlagosítva a fogyasztás kb. ötször magasabb. 1 percnyi repülés 1,6 Mach sebességgel csak 27 kilométernyi táv, gazdaságos sebességgel, azonos üzemanyag mennyiséggel 135 kilométert lehetne megtenni. Tehát minden 1 perc száguldozás 1,6 Mach sebességgel nagyjából 100 kilométerrel csökkenti a hatósugarat, és akkor még a gyorsítás üzemanyag igényét számításba se vettük. A modell használatakor elképzelhető forgatókönyv, hogy a reptértől akár 200-250 kilométer távolságban járőrözik nagy magasságban a repülőgép, póttartályokkal. Amikor szükséges, akkor eldobja a póttartályokat, majd a teljes belső üzemanyag készletével 10 kilométer magasan gyorsít fel és tér haza. Ezzel elérhető akár 350-400 kilométeres hatósugár is, ha a sebességet 1,4 Machra korlátozzuk, meg a felsorolt feltételekkel.

Mi a helyzet reptérről felszállva egy részben vagy végig maximális utánégető teljesítménnyel végrehajtott elfogás esetén? Ebben az esetben reptérről felszállva kell felkapaszkodni 10 ezer méter magasságba, majd gyorsítani szuperszonikus sebesség fölé. A repülőgép üzemeltetési kézikönyvének segítségével kiszámolható, hogy 4 db AIM-7 Sparrow rakétával, tehát fél légiharc-fegyverzettel az F-15C hatósugara végig teljes utánégetéssel az elfogási pontig nagyjából 200 kilométer. Az F-16C vadászgépnek 4 darab AIM-120 rakétával nagyjából ennyi a hatósugara. A sokkal nagyobb méretű és nagyobb belső üzemanyag kapacitással bíró Szu-27 családé ennél kicsit magasabb, de nem sokkal.

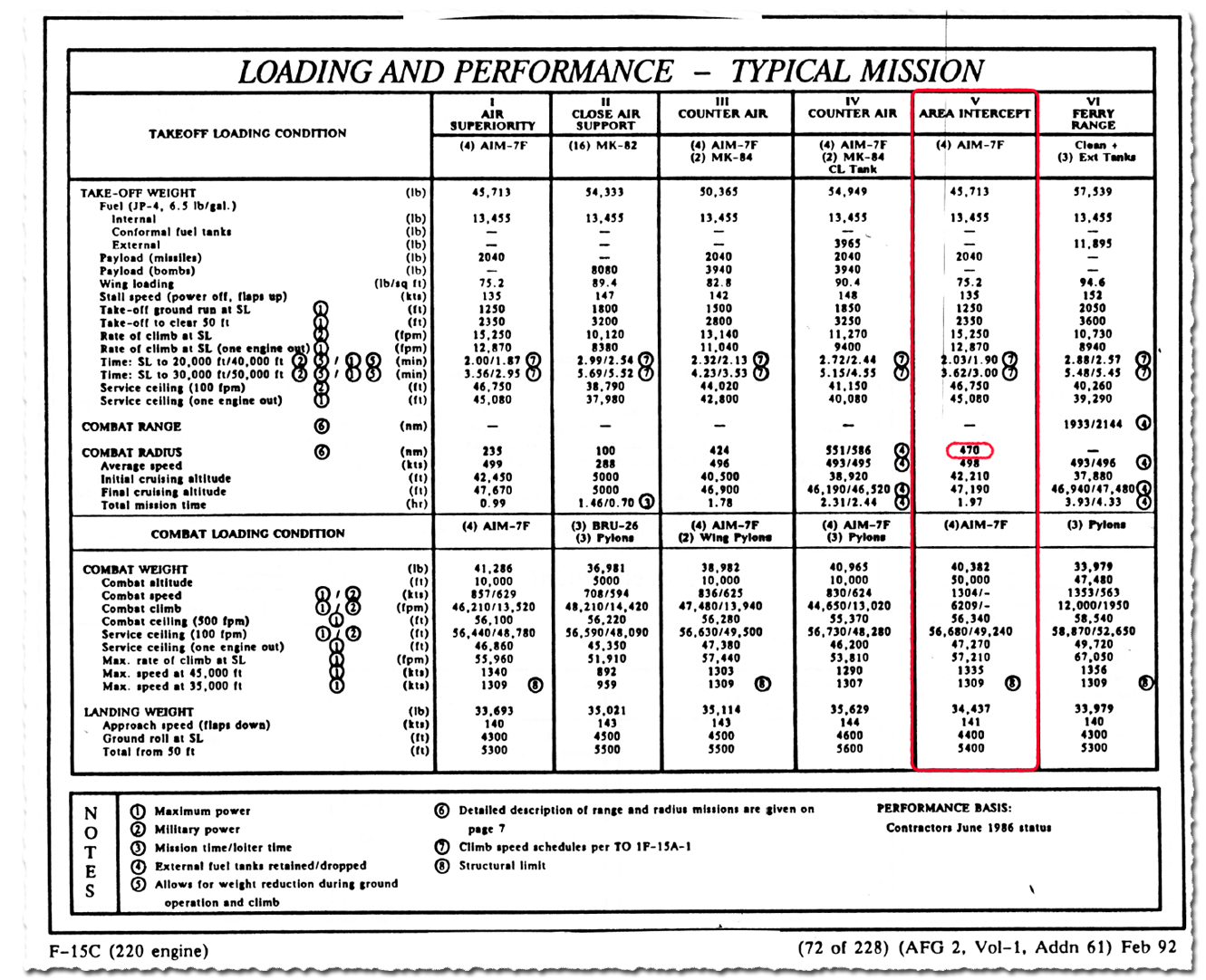
Csak, hogy lássuk a szakadékot a „padlógázas elfogás” és egy moderált, majdnem végig szubszonikus bevetés között. Az F-15C póttartály nélküli szubszonikus hatótávolságára 470 tengeri mérföld, vagyis 870 kilométer van megadva. De ez egy igen konzervatív becslés, mert ez tartalmaz 20 perc várakozási időt és 5% tartalékot, ami 650 fontnyi üzemanyag. Ezen felül nagy magasságú elfogásnál 5 perc maximálgáz tolóerővel is számol a hatósugár számítás. Tehát végig szubszonikus repüléssel és kevesebb tartalékkal, akár 950 kilométeres hatósugár is elérhető, ez teljesen reális. Néhány perc utánégetős gyorsítás és légi harccal is simán megvan a 600 kilométeres hatósugár, póttartályok nélkül is, ha közepes magasságú légiharccal számolunk. A szuperszonikus száguldozásnál semmiféle légiharc nem volt, az elfogás végén egy rakéta indítási lehetőség van, aztán vége a játéknak, lassítani kell majd hazatérni.

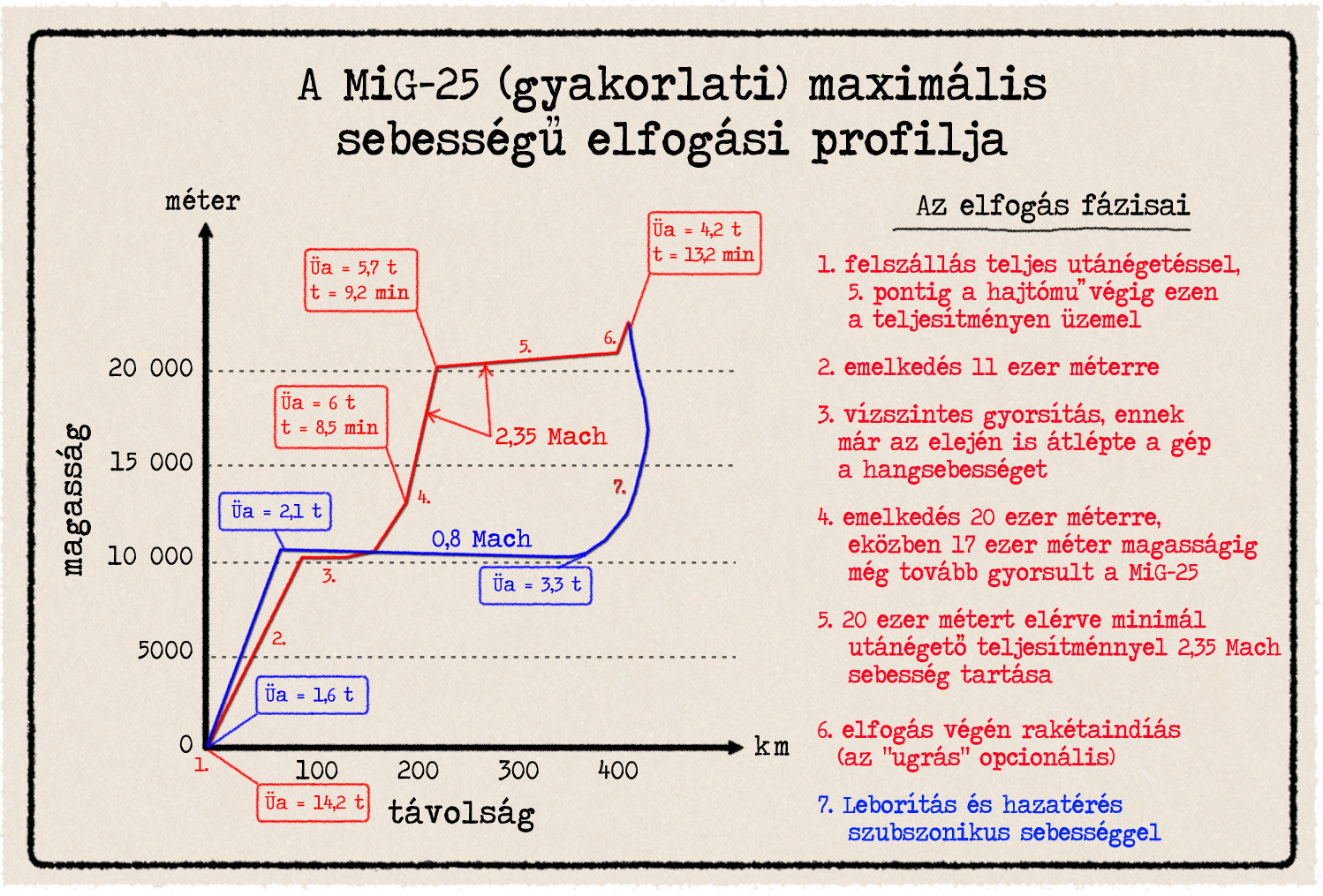
A fenti ökölszámoktól a csúcssebesség és a hatósugarat leszámítva lényegében csak három, valaha is hadrendben levő vadászgép tért el. A MiG-25 és MiG-31 értelmezhető hatósugárral és négy darab nagy rakétával képes volt tartani az 2,35 Mach sebességet kb. 18-20 kilométer magasan. Ez hatalmas méretükből és belső üzemanyag kapacitásukból adódott, lásd az erről szóló anyagot. Az előbbi hatósugara elérte a 400, a másiké a 720 kilométert. Kisebb szuperszonikus sebességgel természetesen a hatósugár értékek még nagyobbak. Az F-15-höz képest mondjuk 1,4 Mach sebességgel a MiG-31 a világból is kirepül úgymond. Ami nem meglepő egy kb. 75%-kal nehezebb vadászgéptől, van benne elég kerozin a mutatványhoz. Csak éppen emiatt alkalmatlan a MiG-31 manőverező légiharcra. A másik kivétel lehet az F-22 és annak szupercirkáló képessége, amiről az extra tartalomban esik szó.

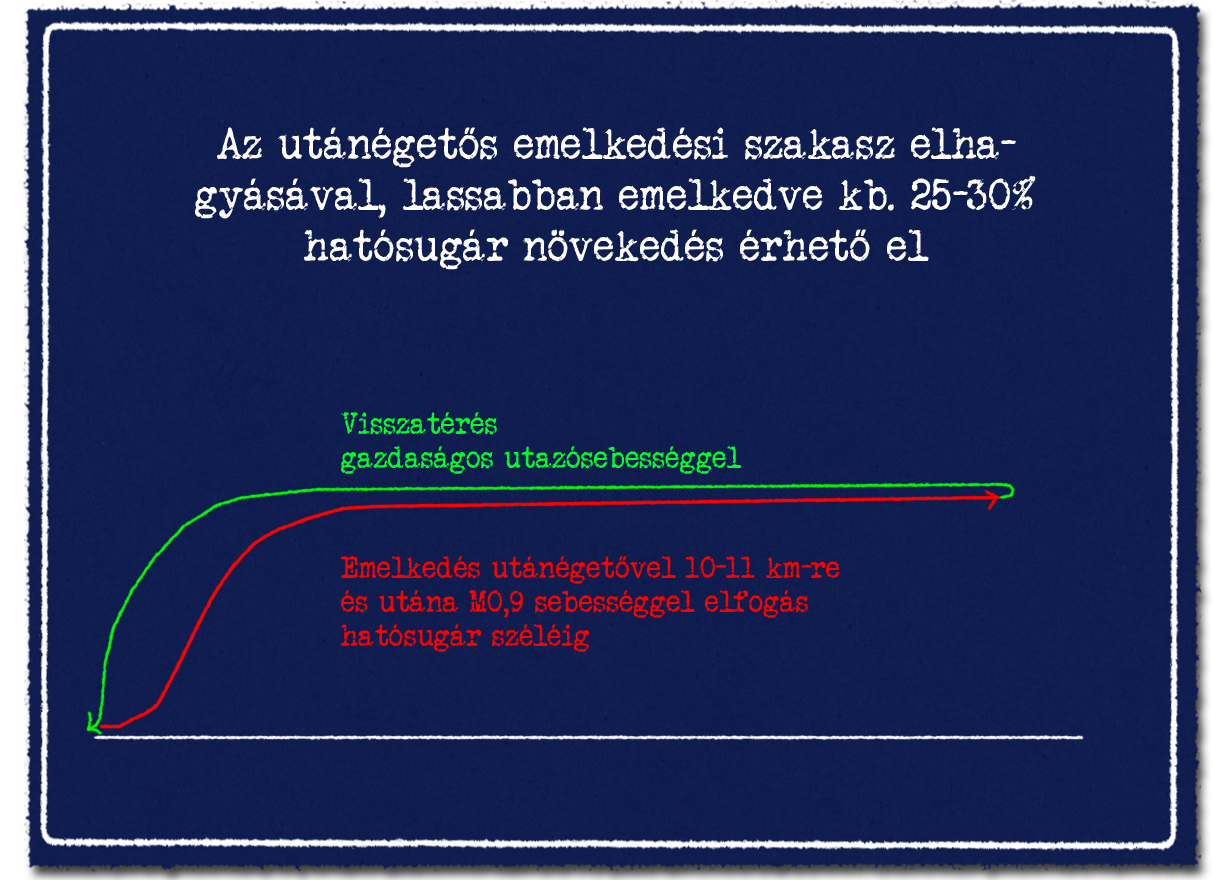
A fentiekből következik, hogy a reptérről végrehajtott elfogások során a nagyjából 10 ezer méterre történő gyors emelkedés során használják a maximális utánégető teljesítményt, majd az elfogás időben és távolságban is döntő részén a maximálgáz, majd hazafelé a gazdaságos hajtómű teljesítménnyel, utazósebességgel térnek haza. Az
F-15 esetén az idealizált szubszonikus elfogás hatósugarának akár 70-75%-a is elérhető, ha csak az emelkedési szakaszban használ utánégetőt. Amennyiben szükséges, akkor nagyon moderált, minimál utánégető és 1,2 Mach táji sebességgel a 100 kilométer nagyságrendű szuperszonikus szakasz is elképzelhető, de azért ez már szabad szemmel látható mértékben csökkenti a hatósugarat. Nem viccből van az, hogy az átlagos, többfeladatú vadászgép élettartamának csak nagyjából. 2%-át (!) tölti szuperszonikus sebesség tartományban. Az iszonyatos üzemanyagfogyasztás egész egyszerűen nem tesz többet lehetővé főleg, hogy nem csak nagy magasságú feladatok léteznek és békeidős légtérhasználati korlátozások is vannak.

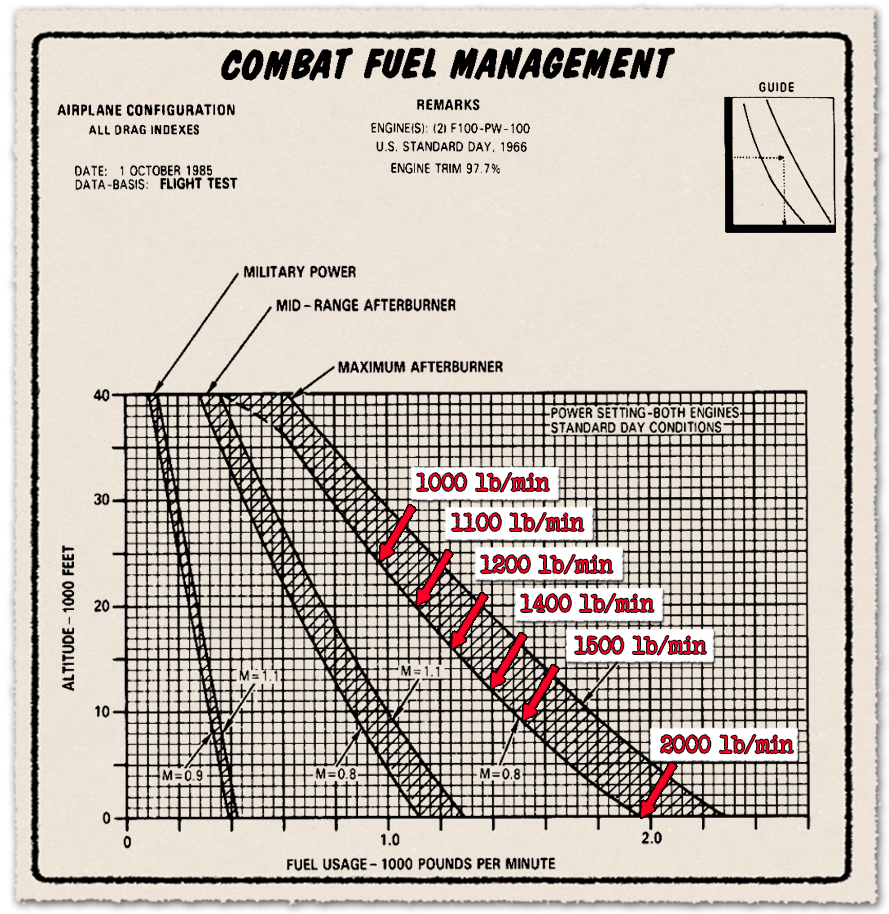
Térjük át a másik estre, amikor az üzemanyag fogyasztás rövid ideig hatalmas lehet, ez a manőverező légiharc. Ekkor nem a nagy sebesség elérése a cél, viszont a nagy túlterhelésű manőverek végrehajtásához szükséges a maximális utánégető hajtómű teljesítmény. A fordulóharcban szükséges hatalmas felhajtóerő előállítása a fordulókhoz hatalmas légellenállással is jár, ezt tolóerővel kompenzálni kell. Ennek fizikai hátterének bemutatása az első részben már megtörtént. A manőverező légiharcok jellemző tartománya a közepes magasság, 3-8 kilométer, vagyis 9-24 ezer láb magassági tartomány. Lássuk a számokat egészen a tengerszinttől.

Tengerszinten 0,8 Mach sebességgel az F-15 percenkénti üzemanyag fogyasztása maximális utánégetéssel kb. 2000 font/perc, tehát nagyjából 1000 liter/perc. Hogy érezzük ennek nagyságrendjét, kb. 5-6 perc alatt felhasználná az összes belső üzemanyagot az F-15A és C változata ezzel a fogyasztással. A növekvő magassággal csökken a tolóerő, tehát a fogyasztás is. De még így is, 12 ezer láb magasságon 1400 font/perc, 16 ezer lábon, 1200 font/perc, 20 ezer lábon 1100 font/perc, 24 ezer lábon 900 font/perc az üzemanyag fogyasztás.

Ezekből az értékekből látszik, hogy ha a manőverező légiharc idejének csak a felében van maximális utánégető teljesítmény, a másik felében csak maximálgáz, akkor sem tarthat 4-8 percnél tovább az intenzív manőverezés időszaka, ha értelmezhető harcászati hatósugár elérése a cél. A magasabb érték inkább csak 5-6 kilométeres vagy nagyobb magasságban igaz.

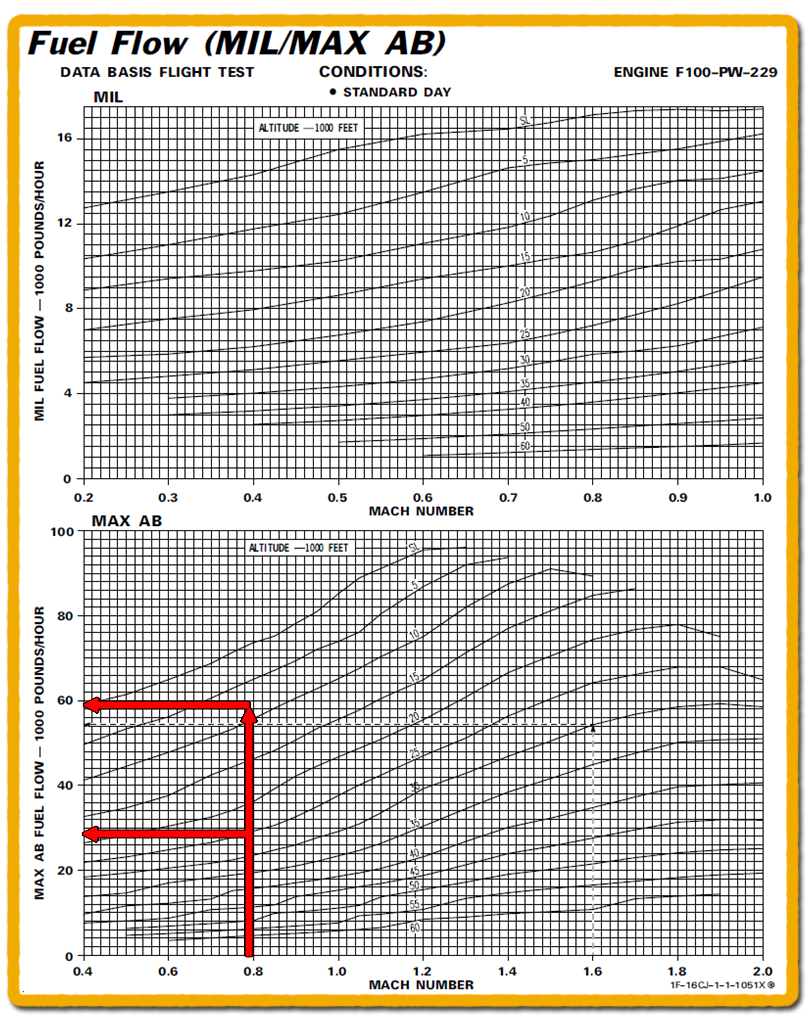
Hasonló következtetésre lehet jutni az F-16CJ vadászgép üzemanyagfogyasztási görbéjét megvizsgálva. A diagram maximálgáz és utánégető teljesítményen is mutatja az F100-PW-229 hajtómű óránkénti üzemanyag fogyasztását. Ezt a hajtóművet használja amúgy több F-15E változat is. A fogyasztás 0,8 Mach sebességnél, nagyjából 10 ezer láb, tehát úgy 3 kilométer magasan 60 000 font/óra, tehát percenként 1000 font. Az F-15 vadászgép ugye kéthajtóműves, ezért van az, hogy ezt a fogyasztást kb. 24 ezer láb magasságában hozza az eggyel korábbi F100 hajtómű változattal. Maximálgáz teljesítményen, hangsebesség közelében a fogyasztás a maximál utánégetős 1/6-a. Az F-16CJ belső kapacitása 7200 font, ennek nagyjából a harmadát szánva légiharcra itt is azt kapjuk, hogy magasságtól függően 4-6 perc intenzív manőverező légiharc lehetséges. Itt is kijelenthető, hogy minden többfeladatú vadászgép átlaga nagyjából ennyi, csodák nincsenek. A fizika még mindig tudja a dolgát.

A tolóerő / tömeg arány és csúcssebesség

Most, hogy már láttuk az elméleti és gyakorlatban alkalmazható csúcssebességeket, no meg a gyorsulásokat, érdemes kicsit visszatérni a tolóerő/tömeg arány részbeni céltalanságához. Nem csak a tolóerő-karakterisztikák, de a lég- és hullámellenállás miatt sincs közvetlen kapcsolat az arányszám és egy vadászgép vagy vadászbombázó csúcssebessége között.

A táblázat értékei alapján látható, hogy mennyire nem írja le jól egy repülőgép csúcssebességét pusztán a fékpadi tolóerő. Hiába jobb az F-15 tolóerő/tömeg aránya a fékpadi értékekkel számolva, mint MiG-25 vagy a MiG-31 típusoké, ettől még sem az elméleti, sem a gyakorlatban alkalmazható csúcssebessége nem éri el azokét. Sőt, az F-15 2,2 Mach csúcssebessége még fegyvertelenül is kisebb, mint az MiG-25 és MiG-31 teljes légiharc-fegyverzettel, gyakorlatban használható értéke, ami 20 kilométer magasan 2,35 Mach. Sokkoló ugye?

Az F-15-öt egyszerűen nem arra tervezték, hogy tartósan nagy sebességgel száguldjon. Cserébe lealázza a két szovjet vadászgépet a közeli manőverező légiharcban, amire meg a másik kettő teljesen alkalmatlan, hiszen nehezek, mint egy darab vas. Az F-15 agyonveri a két nehéz szovjet vasat emelkedés és gyorsulás terén egyszerűen azért, mert pehelykönnyű azokhoz képest. Manőverező légiharcban meg piszkosul jól állít elő felhajtóerőt a szubszonikus sebesség tartományban.

A Foxbat hatalmas, 14,5 tonnás üzemanyag kapacitása ellenére a szubszonikus hatósugara csak 600 kilométer volt. Az F-15C hatósugara utánégetővel 10 kilométer magasra emelkedés, majd végig maximálgáz teljesítménnyel végrehajtott elfogással kb. 600 kilométer. Úgy, hogy az F-15C belső üzemanyag kapacitása csak 5 tonna, lényegében az 1/3-a a MiG-25-nek. Na ennyit számít az, hogy mire és milyen eszközökkel terveznek valamit. Az MiG-25 az optimalizálatlan turbojet hajtóművel ennyit tudott...

Lássuk a következő példát. Az F-111 vadászbombázó család tolóerő/tömeg aránya messze elmaradt a vadászgépekétől, még a legerősebb hajtóművel rendelkező F-111F változaté is. És mégis, az F-111 képes volt elérni nagy magasságban fegyverzet nélkül a 2,2-2,4 Mach sebességet, pont, mint az F-14/F-15 vadászgépek. Viszont ettől még az F-111 gyorsulása nem számított jónak.

Hogy miért, az megérthető, ha a középiskolás F = m*a képletet átrendezzük az a = F/m formára. Az ’F’ ugye az erő, ’m’ a tömeg és az ’a’ a gyorsulás. Az erőt bontsuk szét, ahol repülőgépet gyorsító erő az valójában a tolóerő és a légellenállás különbsége. Ebből átrendezve a gyorsulás a két erő különbsége, osztva tömeggel.
Tehát a = (F_t-F_lé)/m.

Az F-111A egybitang nehéz, de jól optimalizált légellenállású repülőgép volt a variaszárnynak köszönhetően. Tehát a teljesítmény, a tolóerő döntő része a tömeg gyorsítására és nem a légellenállás legyűrésére ment el. Másként: a repülőgép gyorsulása a nagy tömege, az ’m’ értéke miatt alacsony. Az F-15 egy sokkal könnyebb repülőgép, de nem annyira optimalizált a légellenállása szuperszonikus tartományban a variaszárny hiánya és az elvárt szubszonikus manőverező képesség miatt. Kisebb tömeg, de rosszabb légellenállás ellenére is hatalmas gyorsulása van, legalábbis egy pontig. Viszont az a pont, amikor tolóerő már azonos vagy közel azonos, ahol már nem vagy alig gyorsul a repülőgép ugyanazon csúcssebességre adódik az F-111 család és az F-15-nél, ez nagyjából 2,2 Mach. De ettől még a tolóerő és a légellenállási erő különbsége lehet kisebb a köztes tartományban az F-111-nél. Viszont hiába kedvezőbb a légellenállása az F-111-nek, ha a hajtóműveinek sokkal nagyobb tömeget kell gyorsítani, akkor az tovább tart. De a végsebesség ettől még nagyjából lehet ugyanaz.

Egy nagyon egyszerű analógiával élve. Képzeljük el, hogy egy relatíve könnyű kocka formát kell tolni sík felületen, aminek nagy az érdessége. A másik tárgy legyen egy sokkal nagyobb tömegű gömb, amit sima felületen görgetünk. Nagy tolóerőt alkalmazva a láda csúcssebessége gyorsan beáll, mert egy ponton túl eszementen nagy lesz a súrlódás. Ezzel szemben ugyanazon erővel vagy, ha jobban tetszik teljesítménnyel elérhető ugyanaz a haladási sebesség a nehezebb tömeggel is, csak éppen lassabban épül fel a sebesség a nagyobb tehetetlenség miatt. Nagyon kicsi a gördülési ellenállás, csak éppen hatalmas tömeg az, ami görgetni kell.

A tolóerő/tömeg arány egyik legnagyobb problémája az eddig megismertek mellett, hogy a repülőgépek légellenállási tényezője és a homlokfelület nagysága közötti eltérés és annak hatása teljesen rejtve marad. Egy kisebb, egyhajtóműves repülőgép esetén azonos tolóerő/tömeg arány nagyobb vízszintes gyorsulást biztosíthat, mint egy kéthajtóműves gépnél, mert a gép tömeg/homlokfelület aránya, ami a gyorsulást és a légellenállást meghatározza jobb lehet. Emiatt van az, hogy a viszonylag gyengébb tolóerő/tömeg arányú Gripen vadászgép egy F-15-höz képest meglepően jó vízszintes gyorsításra képes. Viszont nagy túlterhelésű forduló és emelkedés, és főleg a kettő kombinációja közben, ahol már gravitáció és a nagyobb felhajtóerő miatti nagyobb légellenállás a fő faktor, ott már szabad szemmel is látható eltérést okoz a két vadászgép között az, hogy akkor mekkora az abszolút tolóerő.

A fajlagos teljesítményfelesleg

Ahhoz, hogy jobban megértsük a vadászgépek paramétereit további diagramokkal szükséges, mondhatni beszélőviszonyba kerülni, illetve megismerkedni a fajlagos teljesítményfelesleg fogalmával. Ez a specific execss power, ezt jellemzően Ps jelöléssel találni meg a teljesítményt bemutató diagramokon. A lehető legtömörebben, hogy mi is ez. Ameddig a Ps pozitív, ott az adott sebesség, tömeg és fegyverzet konfiguráció mellett a helyzeti és mozgási energia összegét képes növelni repülőgép. Tehát képes gyorsulni vagy emelkedni, avagy a kettő kombinációjára is. Ha megkövetelt manővernél a Ps negatív, akkor a repülőgép lassul, illetve a sebesség tartásához süllyedni szükséges.

A Ps lényege, hogy különböző vadászgépek teljesítménye adott pontban objektíven összemérhető. Amelyik repülőgép az adott sebesség és magasságon nagyobb Ps értékkel bír, annak nagyobb a teljesítményfeleslege, amivel még tud gazdálkodni. Pont. Nincs vita.

A fajlagos teljesítményfelesleg fogalom és az értéke azért is jelentős, mert többek között ezt is használták az F-15 elvárt és garantált teljesítmények megfogalmazására, amitől nem maradhatott el. Amennyire tudom ez volt az első vadászgép, ahol ez, mint fogalom szerepelt a szerződéses elvárásban, amit adott magasságon és sebességgel repülve teljesíteni kellett. A fajlagos teljesítményfelesleg nem dimenziótlan érték, de a m/s vagy láb/s értéke ellenére nem a direktben elérhető emelkedési sebességet írja le. Itt és most elégedjünk meg annyival, hogy a nagyobb érték jobb.

Lássuk a fajlagos teljesítményfelesleget diagramon is ábrázolva. A csúcssebesség bemutatásánál használt diagramba rajzolt Ps görbeseregekkel bemutatható a magasság és sebesség hatása a gyorsulásra és emelkedő képességre. Kezdjük a híres hírhedt F-104 vadászgépre vonatkozó diagrammal.

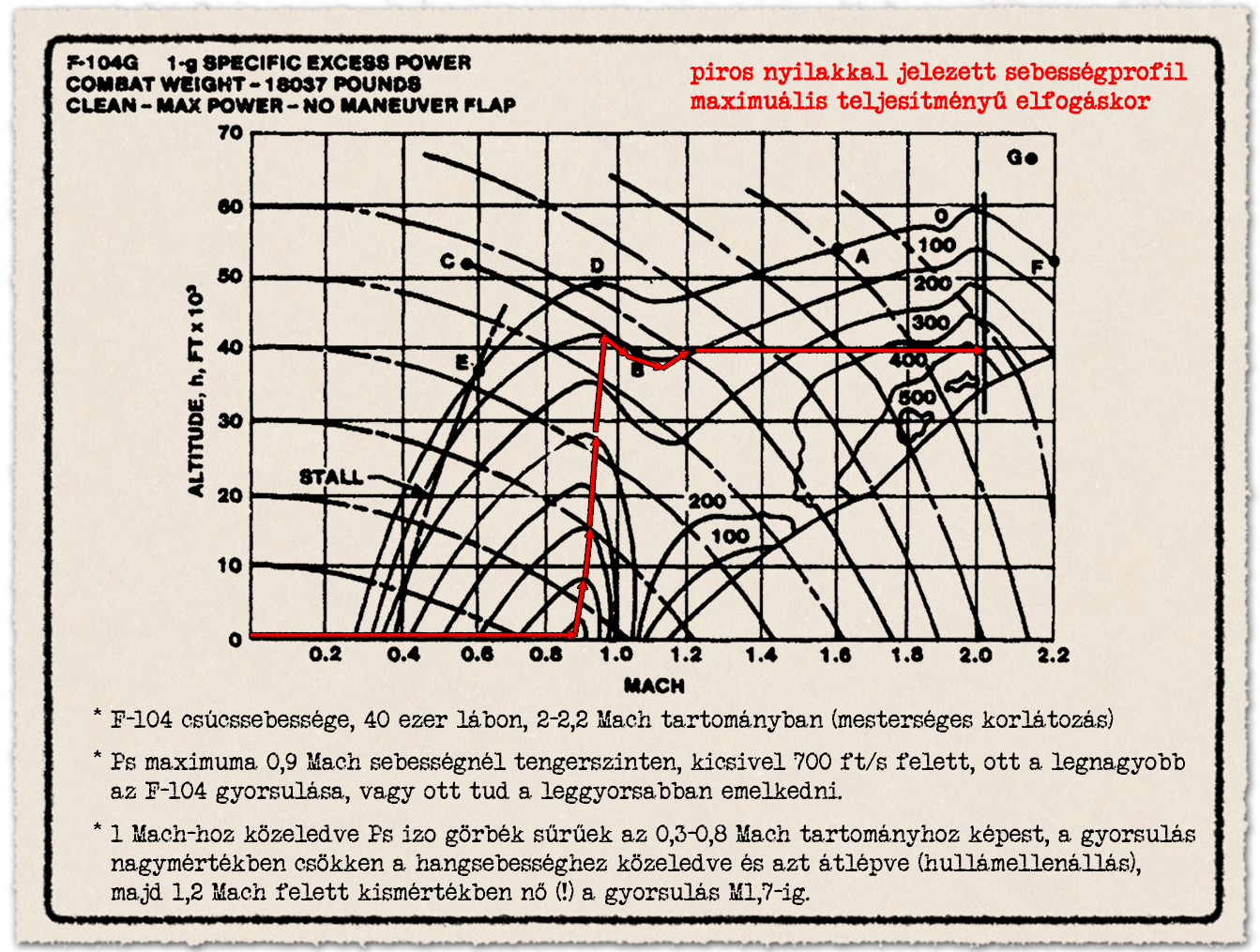
Ahogy gyorsul vagy emelkedik a vadászgép és közeledik a repülőgép sebessége és magassága a Ps = 0 görbéhez, ott már nem gyorsul tovább vagy nem képes emelkedni, tehát eléri a csúcsmagasságot vagy a csúcssebességet. Az F-15 vadászgép csúcssebességének bemutatásakor használt diagramon a görbék a Ps = 0 közeli értéknél érvényes sebesség és magasságot mutatták. Ez az eredeti diagram feletti információkból olvasható ki.

Az F-15-tel összevetve kicsit nagyobb magasságon van az F-104 csúcssebessége, 40 ezer lábon képes elérni a 2 Machot. A Ps érték maximuma 0,9 Mach sebességnél tengerszinten van, valamivel 700-as érték felett. Tehát ott a legnagyobb az F-104 gyorsulása, vagy ott tud a leggyorsabban emelkedni. 1 Mach-hoz közeledve az izo Ps görbék rendkívül sűrűek az 0,3-0,8 Mach tartományhoz képest, ami azt jelenti, hogy a vízszintes gyorsulás nagymértékben csökken a hangsebességhez közeledve és azt átlépve. Ezért a hullámellenállás felel, aminek bemutatása az első részben megtörtént. Ez a fajlagos teljesítményfelesleg értékcsökkenés lényegében minden repülőgépnél hasonlóan néz ki.

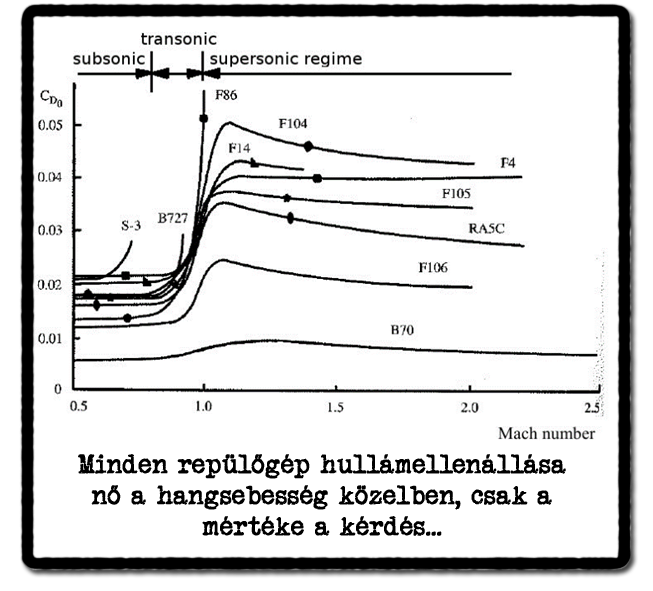
A diagram segítésével levezethető, hogy milyen emelkedési profil célszerű a maximális teljesítményű, vagy emelkedés után végig maximálgázzal történő elfogás esetén. A cél a Ps érték minél magasabban tartása az emelkedés alatt. Tehát felszállás után maximális utánégetéssel gyorsít a vadászgép kb. 0,9 Mach sebességig. Azután olyan bólintási szöggel kell emelkedni, hogy a sebesség csak minimálisan vagy semennyire sem csökkenhet, mert adott magasságon 0,9 Mach táján van a Ps maximális értéke. Ez egyre csökkenő emelkedési szöget jelent, ahogy nő a repülési magasság, hiszen csökken a tolóerő is. 40 ezer láb magasságra kb. ezzel a sebességgel érdemes megérkezni. Amennyiben maximálgázzal repül a vadászgép tovább, akkor innentől fogva nagyjából képes tartani a hangsebességhez közeli sebességet.

Amennyiben szuperszonikus elfogásról van szó, akkor 40 ezer lábat elérve a hangsebesség áttöréséhez érdemes enyhén süllyedni, kihasználva a gravitációt, a felhalmozott helyzeti energiát mozgási energiára váltani. Összeségében megéri egy kevés magasságot feláldozni, hogy az átlag gyorsulás nagyobb legyen. A nagy hullámellenállású tartomány fölé gyorsulva, egyszerre lehetséges a további gyorsítás, lassú emelkedéssel 40 ezer láb magasságba. Ahogy a sebesség nő úgy változik folyamatosan a Ps érték, ami egy ideig még nő is. Tehát az F-104 gyorsulása 1,2 Mach felett egy ideig nő, majd a csúcssebességhez közeledve nagymértékben csökken, ahogy az F-15-nél láttuk az idő-sebesség diagramokon magasságtól függetlenül.

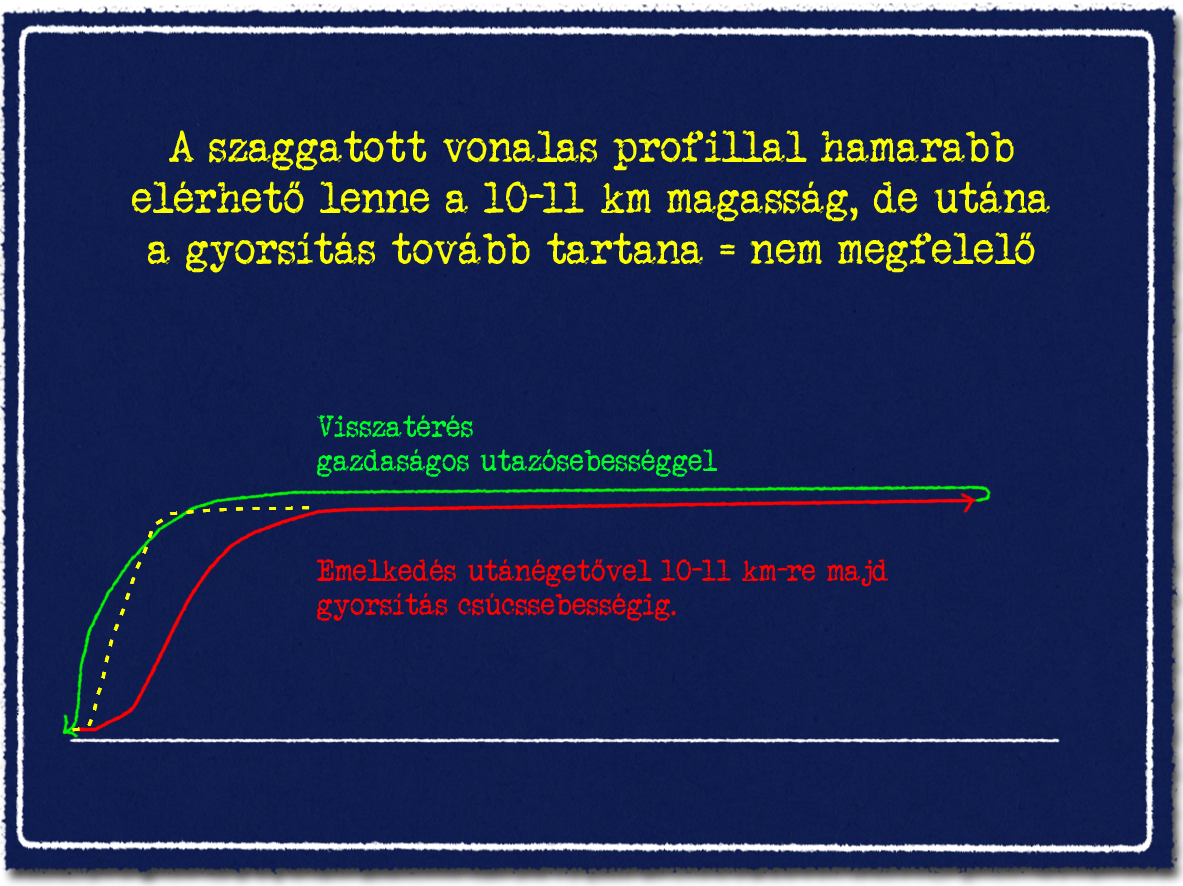
Figyelem, ez a profil nem a legrövidebb idő alatt elérését jelenti a 40 ezer láb magasságnak...! Lehetséges lenne nagyobb emelkedési szöggel hamarabb elérni 40 ezer lábat, csak ebben az esetben egy ponton túl már számottevően lassulna repülőgép. Ha ebből a manőverből hoznák vízszintesbe a gépet, akkor sokkal kisebb sebessége lenne, tehát kisebb Ps értékkel rendelkezne. Emiatt a gyorsítási szakasz a csúcssebesség közelébe sokkal tovább tartana.

A diagram szerint a Ps értéke 0,7 Mach és 40 ezer láb táján 50, ezzel szemben 0,9 Machnál kb. 135 táján van. Az F-15 példáján láttuk, hogy a gyorsulás nagy magasságban mennyivel kisebb a tengerszintihez képest. Emiatt nagyon értékes idő és kirepülési távolságot nézve az a +0,2 Mach sebesség, amit megőriz a lassabb emelkedéssel a vadászgép azért cserébe, hogy nagyságrendileg 15-20 másodperccel később éri el a 10 kilométeres magasság környékét. A támaszponttól számolt kirepülési átlagsebesség nagyobb a valamivel lassabb emelkedéssel, de megtartva a közel hangsebességet emelkedés közben.

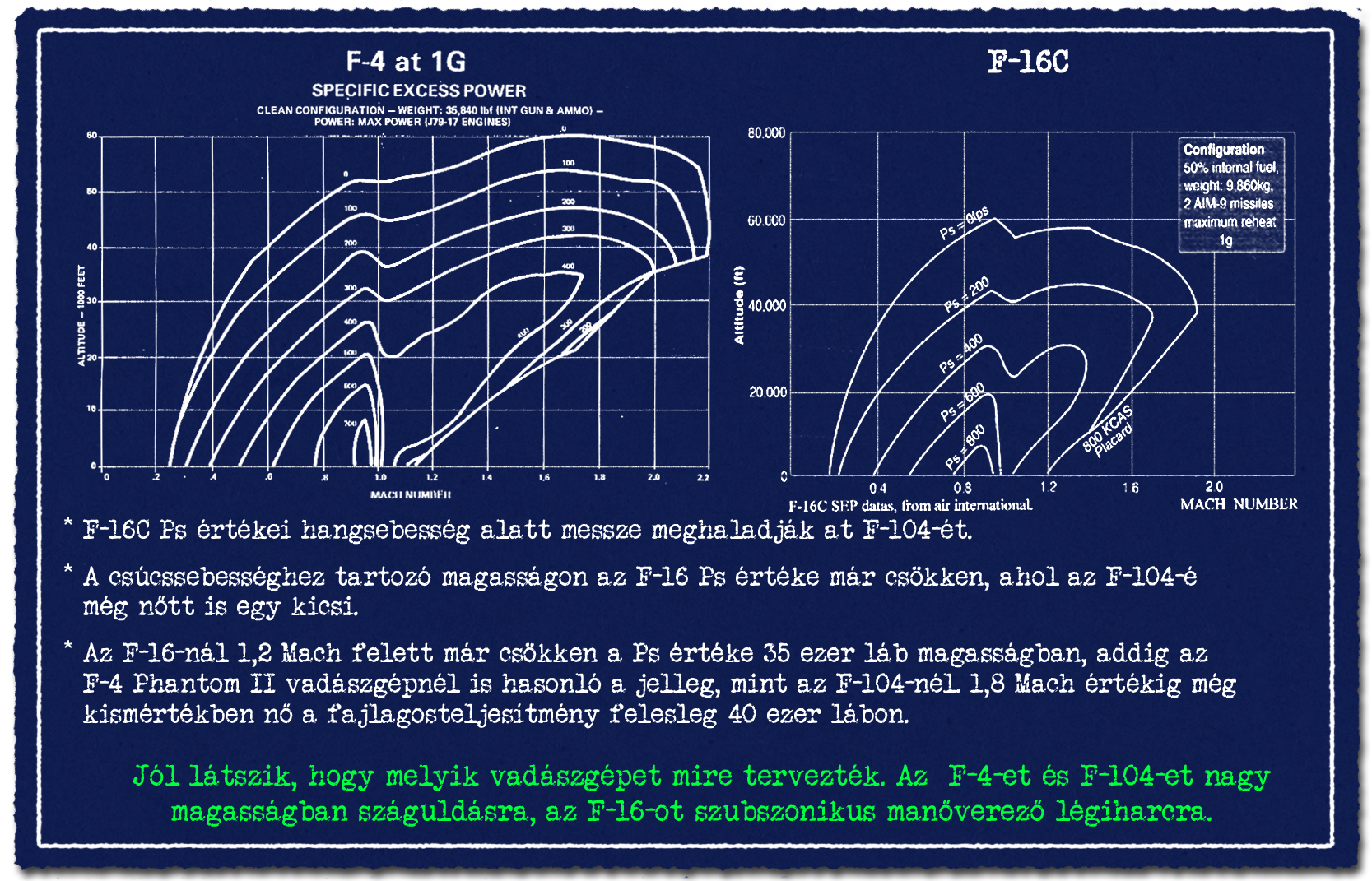
Mire jó még ez a diagram? Például össze lehet vetni, hogy a 4. generációs vadászgépek gyorsulása és emelkedő képessége mennyiben tért el az elődökhöz képest. Már amiről elérhető ilyen diagram. Az F-16C vadászgépnél látjuk, hogy a Ps értékek hangsebesség alatt messze meghaladják a fegyvertelen Starfighter vadászgépét szubszonikus tartományban úgy, hogy két kisméretű rakéta is van az F-16-on. Azonban csúcssebességhez tartozó magasság közelében az F-16 teljesítménye elkezd beesni, a Ps értéke csökken, ahol az F-104-é még nőtt is picit. Az F-16-nál 1,2 Mach felett már csökken a Ps értéke 35 ezer láb magasságban, addig az F-4 Phantom II vadászgépnél is hasonló a jelleg, mint az F-104-nél. 1,8 Mach értékig még kismértékben nő a fajlagosteljesítmény felesleg 40 ezer lábon. Ebből látszik, hogy melyik vadászgépet mire tervezték. Az F-16 a hatalmas tolóerővel, úgymond erőből és nem ésszel éri el a csúcssebességét, addig az F-104-nek a hullámállenállása a nagyobb sebesség elérésére és tartására lett optimalizálva. Az F-104 kortársának tekinthető F-4 Phantom II esetén is jól látszik szuperszonikus repülésre optimalizálás.

Ez a diagram típus magyarázza meg azt, amit az F-15 gyorsulásánál láthattunk még az anyag elején. A Ps érték viszonylag magas marad, majd a csúcssebesség közelében zuhan be. Emiatt volt az F-15-nél kb. azonos a 0,8-ről 2 Mach, illetve a 2-ről 2,2 Mach sebességre gyorsítás ideje. A Ps görbeseregen látszik, hogy melyik tartományban alacsony vagy magas a Ps értéke. Ez a jelenség minden vadászgépnél megjelenik, ahol nem a szívócsatorna korlátozza le a csúcssebességet.

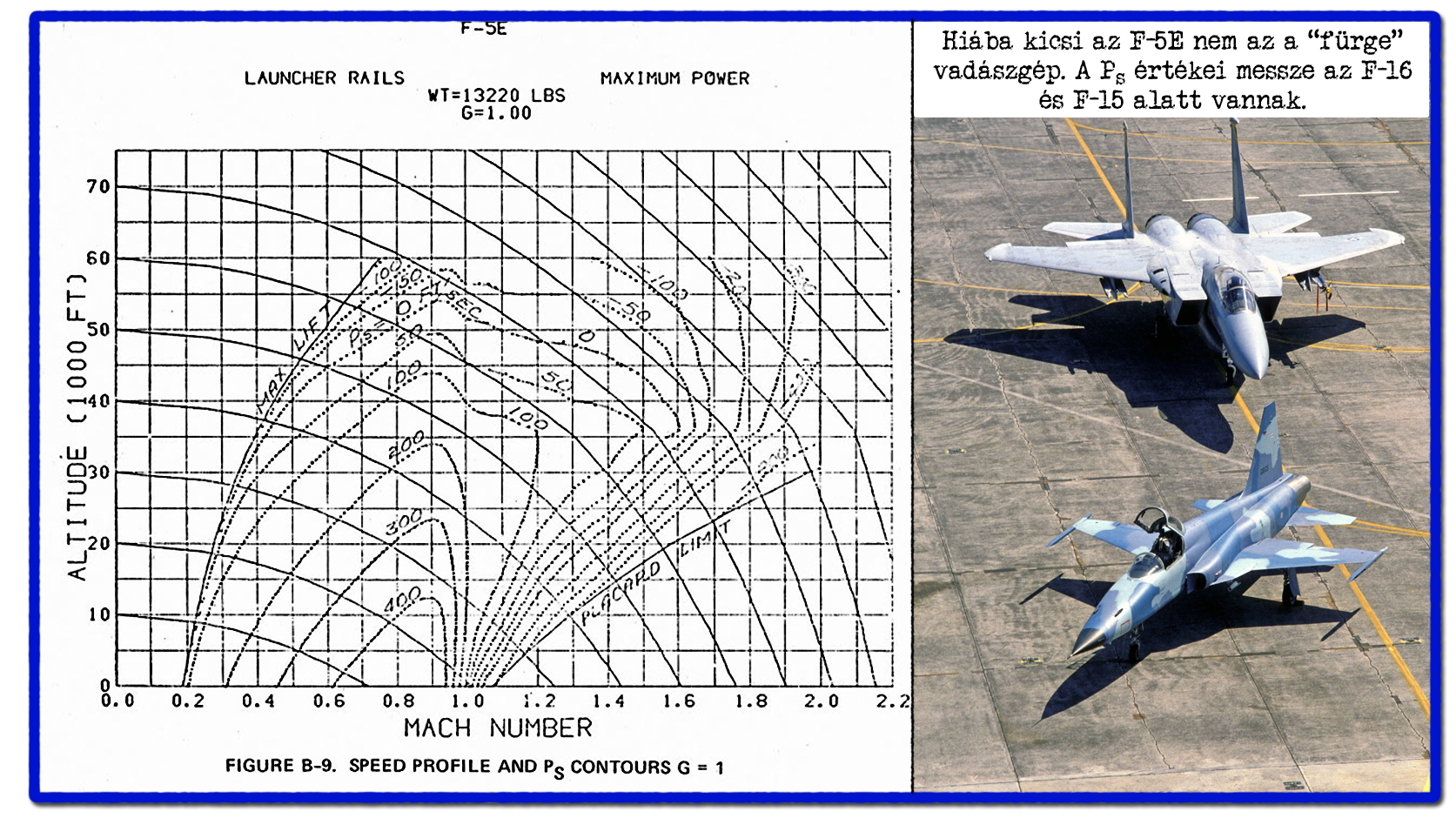
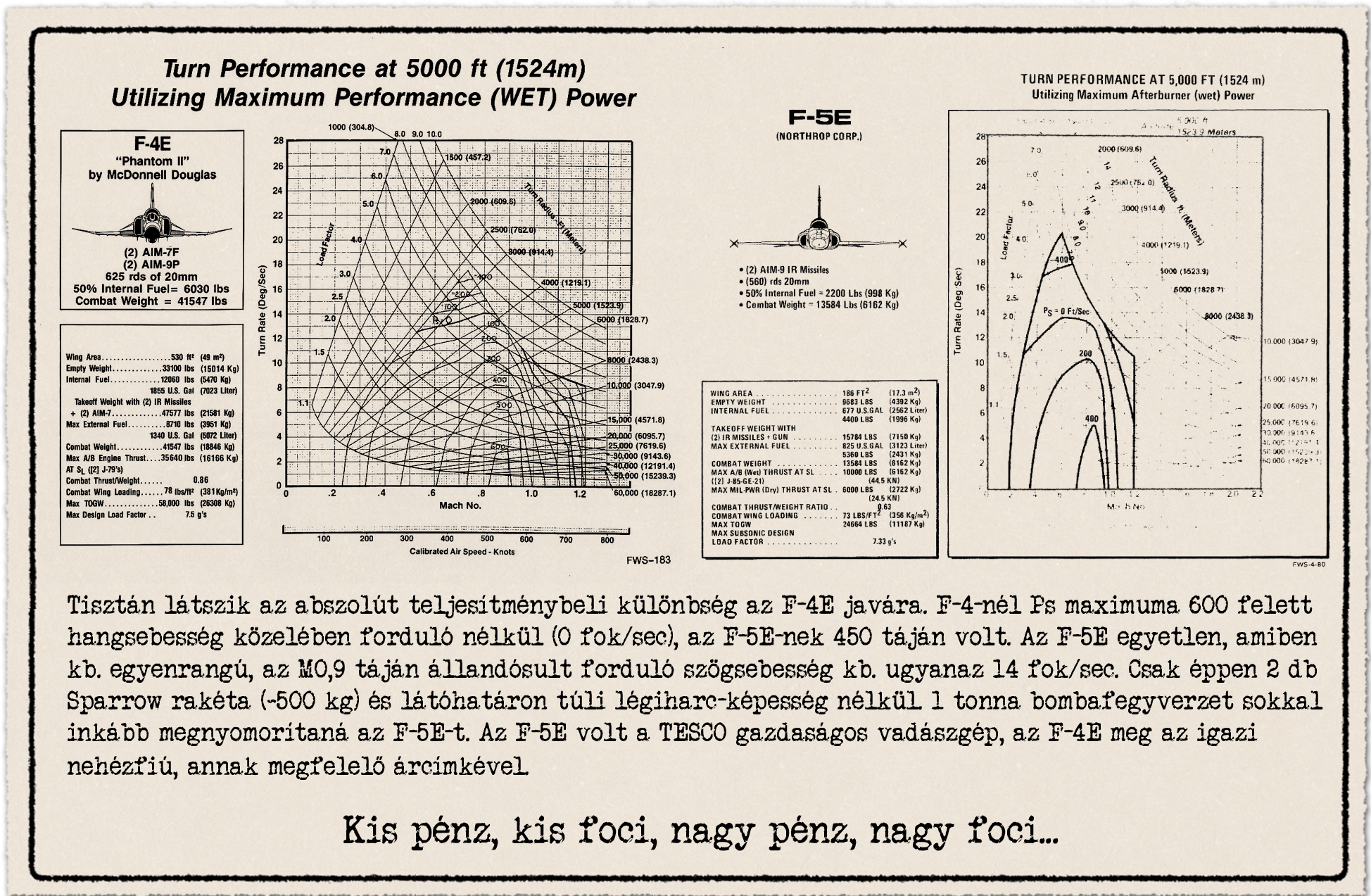
 Mire jó még a fajlagos teljesítmény felesleg? Például az olyan bugyuta és sztereotip kijelentések cáfolatára, hogy „kis agilis, gyors vadászgép”. Attól, hogy egy vadászgép kis méretű semmilyen szinten nem következik, hogy jól gyorsul, jól emelkedik vagy képes-e gyorsan fordulni. Az F-5E vadászgép Ps értékeiből tisztán látszik, hogy kis tömeg és méret ide vagy oda, közelében nincs királykategóriához képest könnyűnek számító F-16 repülési teljesítményéhez sem. Az F-5E egy nagyjából 4,5 tonnás vadászgép az F-16 változattól függő durván 7,5-8 tonnájához képest. De mindez még semmi. Hiába 12,5 tonna egy F-15A és 16 tonna Szu-27, attól még, hogy sokkal nagyobbak és nehezebbek valójában ezek a „fürgék”. Jobban gyorsulnak, jobban emelkednek minden sebesség és magasság tartományban a pöttöm és pehelykönnyű F-5-höz képest. Azért, mert eszementen nagy tolóerővel bírnak és a generációs ugrást jelentő aerodinamikai megoldásokkal ennyivel hatékonyabban állítják elő a felhajtóerőt. Ez persze az árukon is meglátszik. Hát igen, nagy pénz, nagy foci...

Térjünk vissza az F-15 vadászgéphez, aminek a négy diagramja majd segít rátérni a következő témára. A bal felső sarokban részben semmi új, az 1G túlterhelésre, vagyis vízszintes repülésre vonatkozó Ps értékek láthatók kb. 50% üzemanyaggal, maximális utánégetéssel egy fegyvertelen F-15C vadászgépnél. Ennek külső burkoló görbéjét már jól ismerjük. Mi az, amit látunk? Kimagasságon a Ps értéke meghaladja az 1000-et. Ez kéremszépen a királykategória. Az F-15, gyorsul, mint az olajozott istennyila és emelkedik, mint egy űrrakéta, ha kell. Viszont az F-104-hez hasonlóan itt is látni, hogy hangsebeség közelében eléggé bezuhan a Ps értéke, mert ugyanazon fizika vonatkozik minden repülőgépre. Isten hozta ismét kedves hullámellenállás...

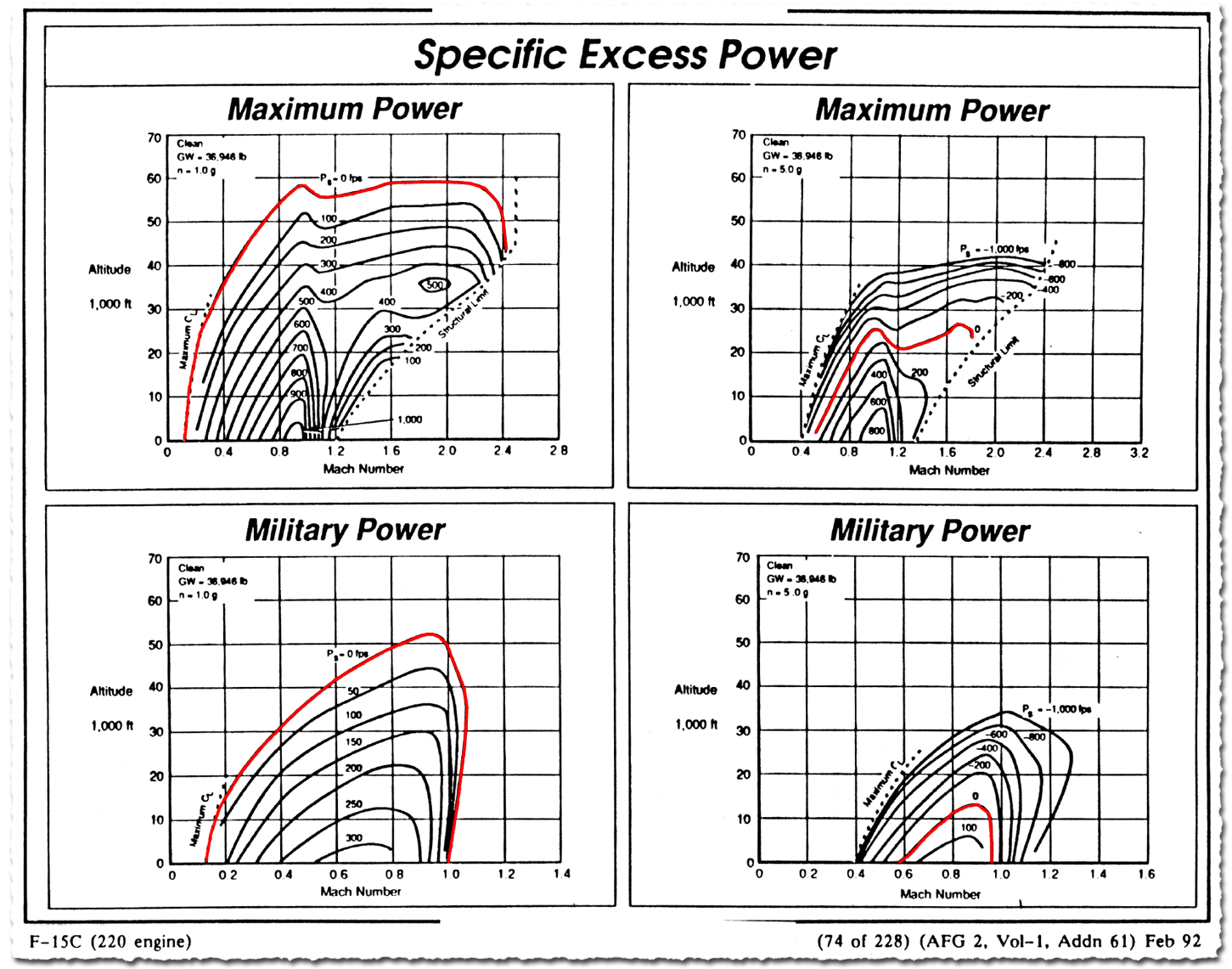
A baloldalin alul a maximálgáz teljesítményen, a Ps értékek számottevően kisebbek. A diagram érdekessége, hogy az F-15 fegyvertelenül képes tartani a hangsebességnél alig nagyobb sebességet, erről a témáról bővebben az extra tartalomban. Ez a diagram nem mond ellent a korábbinak a rajta szereplő görbék ellenére.

Lássuk a következő két diagramot, amik nem a tipikusan használtak közé tartoznak, jobb oldalt. A korábbiakhoz képest az 5G túlterhelésű fordulóban elérhető csúcssebesség és Ps értékek látszanak rajtuk, felül utánégetővel, alul maximálgáz teljesítménnyel. Látható, hogy a forduló teljesítményigénye mennyire összenyomja azt a sebesség és magasság tartományt, ahol az F-15 mozgási és helyzeti energiája nem változik, ahol a Ps értéke 0.

Teljes utánégetővel 30 ezer lábon 0,9 Mach sebességnél vízszintes repülésben a Ps értéke 500, addig 5G-nél már negatív. Tehát ebben a magasságban egy 5G-s forduló már csak magasságvesztéssel hajtható végre, ha a sebesség tartása a cél. Nagyjából 25 ezer láb és 0,9 Machoz közeli sebesség az, ahol az F-15 sebessége nem csökken egy 5G-s vízszintes fordulóban, a megadott tömeggel. Több üzemanyaggal és fegyverzettel, vagy kisebb magasság, vagy kisebb túlterhelés szükséges a sebesség tartásához. Maximálgáz teljesítményen a sebességvesztés nélküli 5G-s forduló 0,9 Mach és kb. 13 ezer láb magasságban van. Ilyen brutális hatása van a maximál utánégető teljesítmények a manőverezőképességre.

Azonban ez a diagram típus nem igazán alkalmas és nem is túl gyakran használt a vadászgépek forduló és emelkedő képességének meghatározásra, mert csak egyetlen túlterhelése vonatkozik. Ez inkább csak annak a bemutatására hasznos, hogy a teljesítmény szélső értékei hogyan nyomodnak össze vízszintes repüléshez képest. Szerencsére létezik ennél sokkal alkalmasabb diagram típus a célra, nem is egy, lássuk hát ezeket.

 Vadászgépek forduló képessége

Annak ellenére, hogy a vadászgépek ritkán fordulnak csak vízszintesen és állandó szögsebességgel, a könnyebb összehasonlíthatóság és értelmezhetőség miatt erre szoktak adatot vagy diagramokat megadni, hogy az adott vadászgép teljesítménye összehasonlítható legyen. Mondhatni ez a viszonyítási pont, ami valójában igazából nem is pont, hanem ez is karakterisztika jellegű mutató. A fordulóknál jól értelmezhető értékek a túlterhelés, fenntartható forduló szögsebesség, illetve a fordulósugár. Első lépesben foglalkozzunk ezekkel. Az F-15 vadászgépnél az eddig már többször vizsgált, három konfigurációval nézzük meg a fenti három paramétert.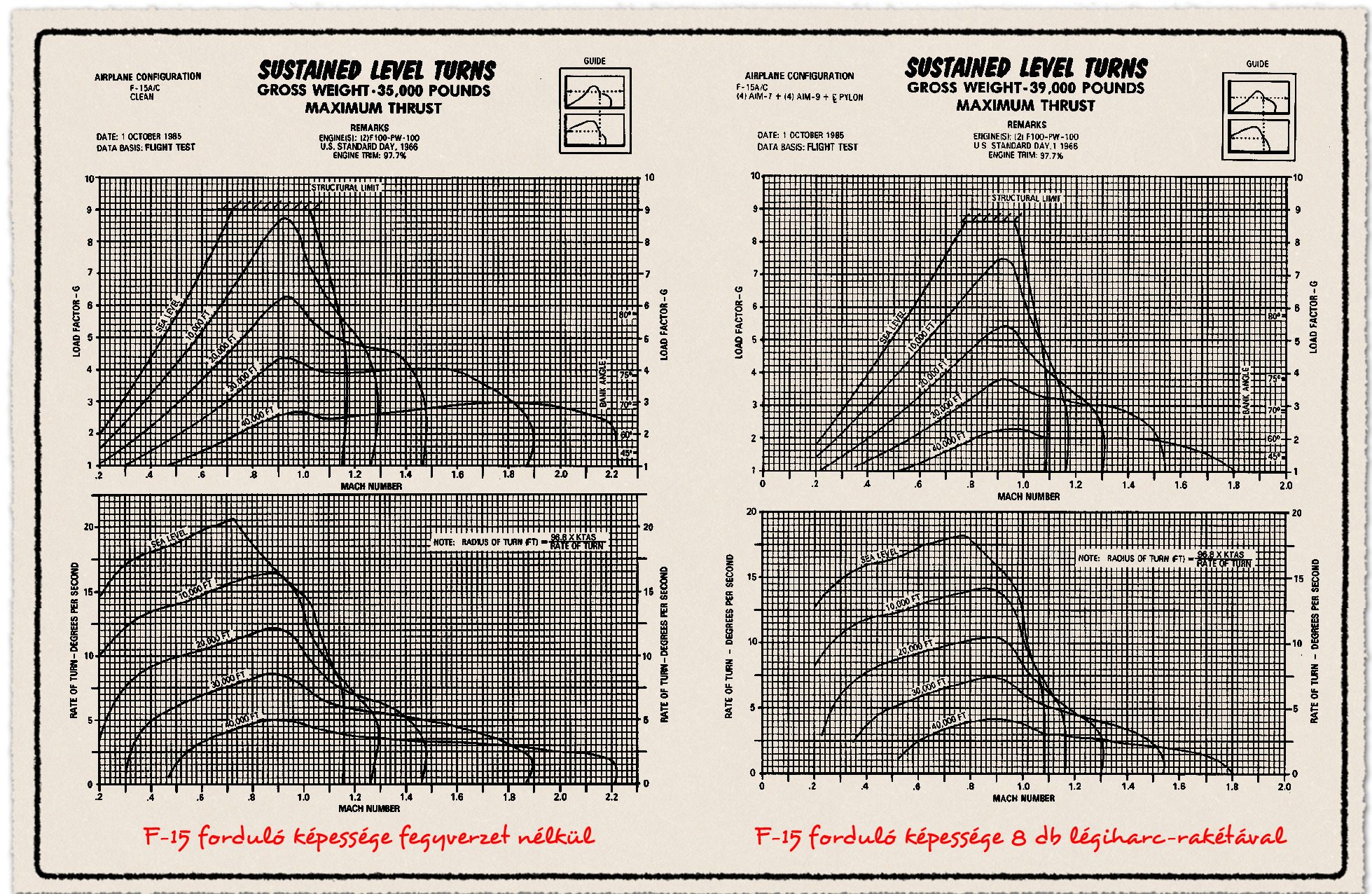 

A diagram felső részén a fenntartható vízszintes forduló szögsebesség van ábrázolva a sebesség és magasság függvényében. A fenntartható vízszintes forduló szögsebességnél a vadászgép nem veszít sebességet, és nem változtat magasságot. Tehát ezek a paraméteres görbék valójában a Ps = 0 értékű görbék is egyben. Ameddig a korábban használt diagram csak egy túlterhelésnél mutatta a Ps értékeket változó magasság és sebességnél, itt az eltérő sebesség és magasság hatása van ábrázolva a Ps = 0 karakterisztikára.

Az F-15 függesztmény nélkül, tengerszinten 0,7 Mach mellett már képes a maximális 9G túlterhelésű fordulóra maximális utánégetéssel, képes előállítani a szükséges felhajtó- és tolóerőt. Ez egészen hangsebességig érvényes marad, sőt, a túlterhelés lehetne nagyobb is. Az F-15 engedélyezett maximuma 9G, ezt mutatja a structural limit vonal. Ez persze nem jelenti azt, hogy a típussal rövid időre nem érthető el és nem húztak bele a gépekbe adott esetben ennél nagyobb túlterhelést...

A hangsebességhez közeledve és átlépve leesik a forduló szögsebesség minden magasságon. Ez sem meglepő, hiszen az 1G túlterhelést bemutató diagramnál láttuk, hogy a hullámellenállás miatt még vízszintes repüléskor is beesik a Ps ebben a sebességtartományban. Tehát a forduló végrehajtására is kisebb a teljesítmény felesleg marad. A csúcssebesség felé közeledve is egyre csökken a forduló szögsebesség, hiszen a tolóerő egyre nagyobb része szükséges pusztán a sebesség megtartásához, tehát csak kisebb szögsebességű és túlterhelésű forduló lehetséges amennyiben a sebesség megtartása szempont.

A paraméterezett görbéken jól látszik növekvő magasság hatása. A fenntartható forduló szögsebesség csökken azonos sebesség és növekvő magassággal. Ez a magassággal csökkenő tolóerő és a ritkább légkör miatt van. A repülőgép kevesebb felajtóerőt képes előállítani, ráadásul a tolóerő meg egyre kisebb. Ennek hatása egészen drámai, 10 kilométer magasan, 30 ezer láb táján egy fegyvertelen F-15 teljes utánégető teljesítménnyel kb. 50% üzemanyaggal is csak 4G túlterhelést képes sebességvesztés nélkül tartani. 13 km magasságban már csak nagyjából 2,5G-t. Mit jelentek ezek az értékek a fordulás sebességét, illetve a fordulósugarat tekintve?

A diagram alsó részén az adott sebesség és magasságon és adott túlterhelésű forduló melletti forduló szögsebesség olvasható le. 0,7 Mach sebesség és 9G túlterhelésnél ez kb. 21 fok /másodperc. Tehát egy teljes 360 fokos forduló végrehajtása kb. 18 másodpercet vesz igénybe. Azért csak kb., mert figyelembe kell venni, hogy a bedöntésnek és az állásszög növelésének, majd a forduló végén a vízszintesbe hozásnak is van időszükséglete. A fordulósugár számítása látható a diagrammon, tengerszinten a hangsebesség 340 m/s, ami 660 csomó. 0,7 Mach sebességnél és 9G túlterhelésnél ez 650 méter. Annak, aki látott már valaha repülőnapon vadászgépet bemutatót repülni, ebben semmi rendkívül nincs. Egy vadászgép a maximális teljesítményével képes rendkívül gyorsan és kis területen megfordulni.

Mi a helyzet nagy magasságban? 13 kilométer, 40 ezer láb magasságban 0,9 Mach sebességnél a forduló szögsebesség csak 5 fok, a hangsebesség 295 m/s, ami 560 csomó, tehát a forduló sugár kb. 3,1 kilométer. Mivel a repülőgép tengerszinthez képes nagyobb sebesség mellett lassabban fordul, emiatt hosszabb a megtett út, vagyis nő a fordulósugár. Kétszeres hangsebességnél 40 ezer láb magasságban a forduló szögsebesség már csak 2,5 fok/másodperc, a túlterhelés kb. 2,8G. De még ekkora sebességnél is csak 14 kilométer a fordulósugár, viszont kicsivel több, mint 2 percig tart a forduló, miközben a gép cirka 43 kilométert tesz meg.

A 2 Mach sebességhez tartozó forduló sugarat csak azért mutattam meg, mert még a ’90-es években hangoztak el a médiában és sajtóban olyan ostoba kommentek, hogy minek Magyarországnak olyan vadászgép, ami a magyar légtérben alig képes megfordulni. A számokból látszik, hogy nincs olyan vadászgép, amire ez az egetverően ostoba kijelentés igaz lenne, még nagy magasságú és sebességű forduló esetén sem, aminek a harcászati realitása nagyjából tart a zéróhoz.

A fentiekből az is látszik, hogy okkal van az, hogy a közeli manőverező légiharc jellemzően közepes magasságon zajlik. Még, ha valami furcsa módon 10 ezer méteres magasságban kezdődne egy ilyen, a nagy túlterhelésű fordulók teljesítmény igénye miatt a vadászgépek süllyedés közben hajtják végre a fordulót, hogy a sebességük ne csökkenjen le rövid idő alatt. Ez amúgy igen jól látszik a híres hírhedt felvételen, amikor a Sivatagi Vihar hadműveletben egy F-16-os egy KUB rendszer által indított rakétákat manőverezett ki. Az első indított rakétát még 26 ezer láb, tehát nagyjából 8 kilométer magasan manőverezte ki a pilóta nagy túlterhelésű fordulóval, addig a videó végén a magasság 10 ezer láb, vagyis 3 kilométerre csökkent. A helyzeti energia, vagyis a magasság feláldozásával sikerült a fordulók végrehajtásához szükséges sebességet megtartani. Úgy ahogy...

https://youtu.be/2uh4yMAx2UA?t=187

A repülési teljesítmény még mélyebb megértéséhez szükséges megismerni a különféle módon definiált sebességeket. A repülőgépek haladási sebességét többféle módon lehet meghatározni, ennek hatása látszik amúgy a bevágott F-16 HUD videón is. A szemfülesebbnek feltűnhet, hogy a sebesség 0,9 Mach mellett a HUD bal oldalán csak 380 csomó 25 ezer lábon, amikor itt a hangsebesség kb. 600 csomó. 380 csomós sebességnél nem 0,63 Mach-nak kéne lennie a sebességnek? Hát nem.

A HUD-on megjelenő C betű azt mutatja, hogy a CAS, vagyis a Calibrated air speed, magyarul műszer szerinti repülési sebességet jelzi ki a HUD. A műszer szerinti sebesség a repülőgépen ébredő erőkkel van kapcsolatban. Azonos műszer szerinti sebességnél a repülőgép szárnyain kvázi ugyanakkora felhajtóerő ébred azonos állásszögnél. Ez a megközelítés igaz a légellenállásra is. Ez a manőverező légiharc szempontjából fontos, mert szemléletesen jelzi a pilóta számára a repülőgép vezethetőségének és manőverező képességének a határait.

A magasság emelkedésével azonos földhöz képesti sebesség vagy azonos Mach-szám esetén műszer szerinti sebesség egyre kisebb a ritkább levegő miatt. Létezik természetesen erre vonatkozó diagram, de aki csak nagyságrendileg szeretné tudni, hogy a légkör hogyan befolyásolja ezt, akkor azt különféle online számoló alkalmazásokkal megteheti. Link a leírásban ehhez.[1]

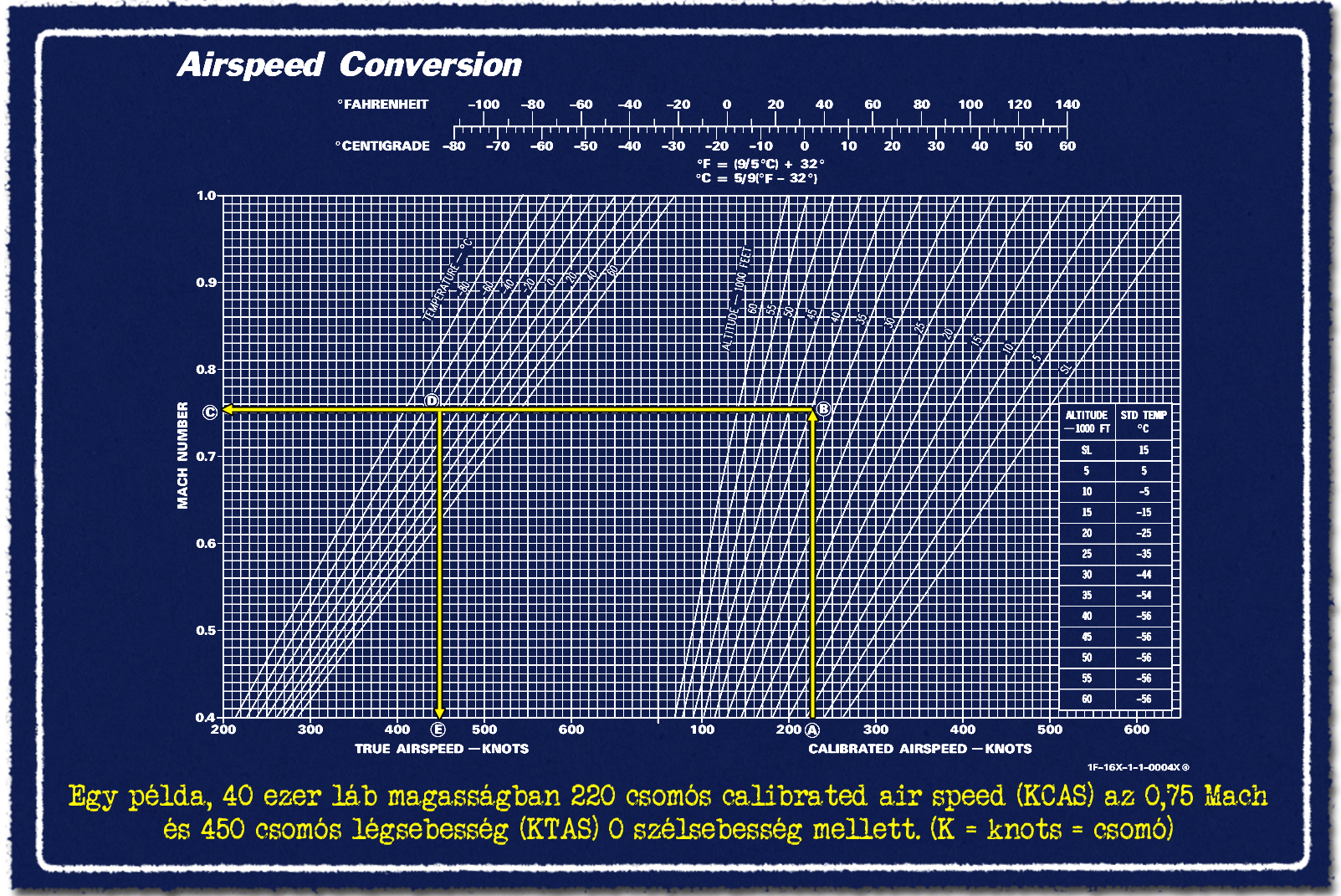
Ha a HUD-on a T betű látszódna, akkor a HUD True air speed, vagyis a légsebességet mutatná. Ennél a változó sűrűség és a levegő összenyomhatóságából származó hatások korrigálva vannak, de a szélsebesség hatása nem. Ez mutatja a repülőgép haladási sebességét a környező levegőhöz képest. Tehát, ha egy a talajhoz képest 400 km/h-val repülő gépnek 50 km/h-s ellenszele van, akkor légsebesség 450 km/h. Emiatt szinte soha nem egyezik meg a föld feletti sebesség a légsebességgel. A légsebesség a navigáció számára fontos, hogy mért szélsebességgel kombinálva számolható legyen a földfelszínhez képesti haladási sebesség, angolul ez a ground speed. Ezekkel majd a navigációval és a bombázással kapcsolatos anyag foglalkozik majd bővebben.

Vissza a diagramokhoz. Azok egymásnak megfeleltethetősége jól látszik. Annak ellenére, hogy ez a diagram forduló képességről szól, az 1G túlterherlés, vagyis a vízszintes repüléshez érve a pontok a repülőgép csúcssebesség burkológörbéjén levő pontokkal egybeesnek. Pórisasan szólva ezek a diagramok valójában térben is elképzelhető diagramok síkmetszetei.

A gépek forduló képességének bemutatására azonban összetettebb diagram típus is létezik, ahol nem csak a vízszintes, állandó szögsebességű forduló, a Ps = 0 eset van ábrázolva, hanem az attól eltérő esetek is. Ezek több ok miatt is hasznosnak.

Egyrészt, a repülőgépek képesek a fenntartható szögsebességnél is gyorsabban fordulni azon az áron, hogy vagy magasságot, vagy sebességet vesztenek. Az F-4 Phantom II és az F-5E forduló teljesítményét bemutató diagramon szerepel a Ps = 0 görbe, viszont látszik, hogy egy adott sebesség és magasságon, a feltüntetett tömeg mellett mi a legnagyobb elérhető forduló szögsebesség. Természetesen ezt a gép nem tudja fenntartani, mert ahogy csökken a sebessége, úgy csökken ez a csúcsérték is. De össze lehet hasonlítani, hogy annál pontnál, amikor már elfogy a felhajtóerő tartalék mekkora a Ps értéke a vadászgépeknek. Amelyiknek a negatív értéke nagyobb, az lassul jobban, vagy annál kéne nagyobb sebességgel süllyedni a forduló közben, hogy a vadászgép ne lassuljon.

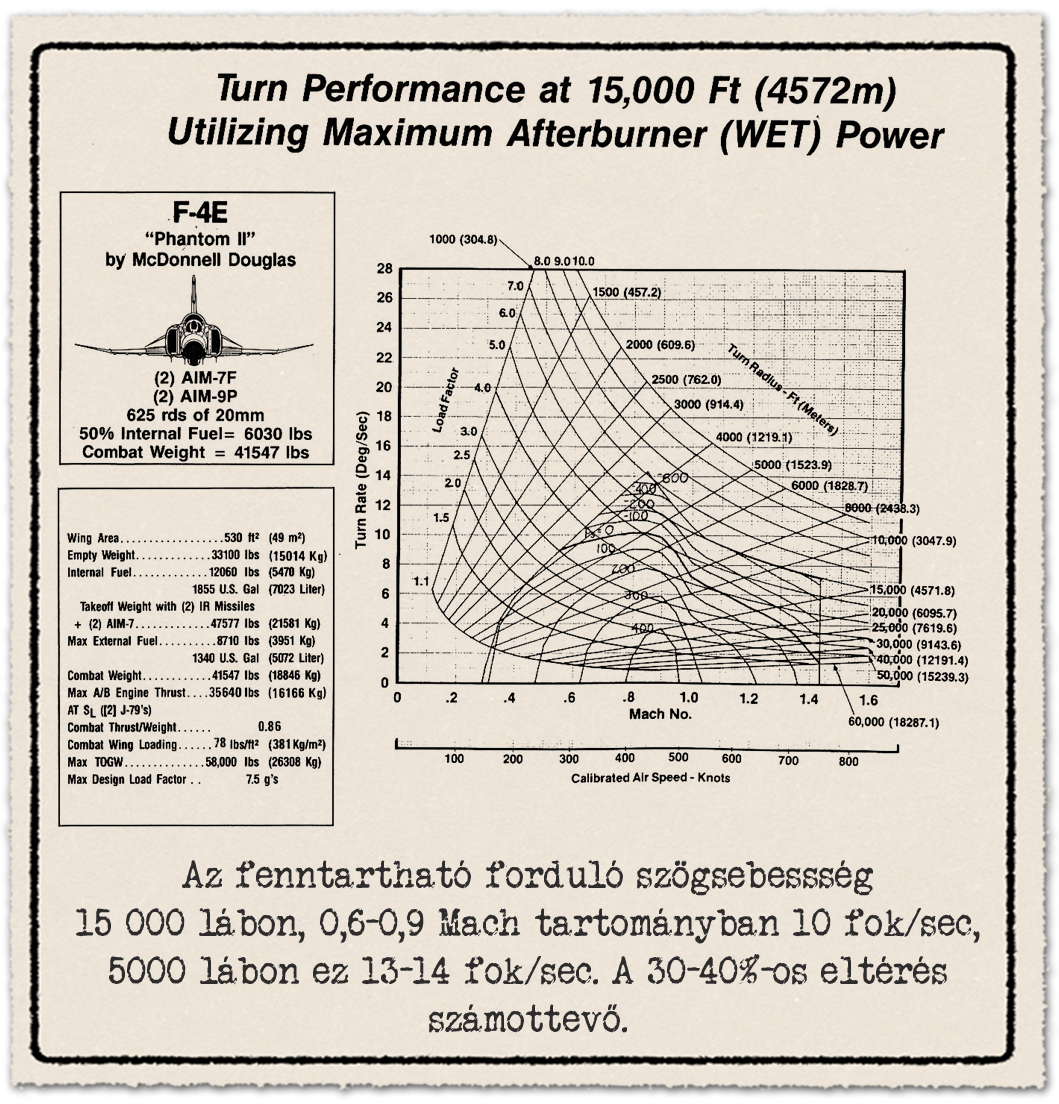
A diagram abból a szempontól is használhatóbb, hogy egyetlen ábrán leolvasható a túlterhelés, forduló szögsebesség és a fordulósugár is. Valójában ezek ugye kötött értékek, egymástól függenek. Valójában a kérdés az, hogy ebben a „mezőben” a repülőgépek Ps értékei hogyan alakulnak. Az eltérő magasságra vonatkozó görbéken itt is látható a már megismert jelenség, nem csak a fenntartható forduló szögsebesség, de az elérhető maximum is csökken, hiszen kevesebb felhajtóerőt lehet előállítani a növekvő magassággal.

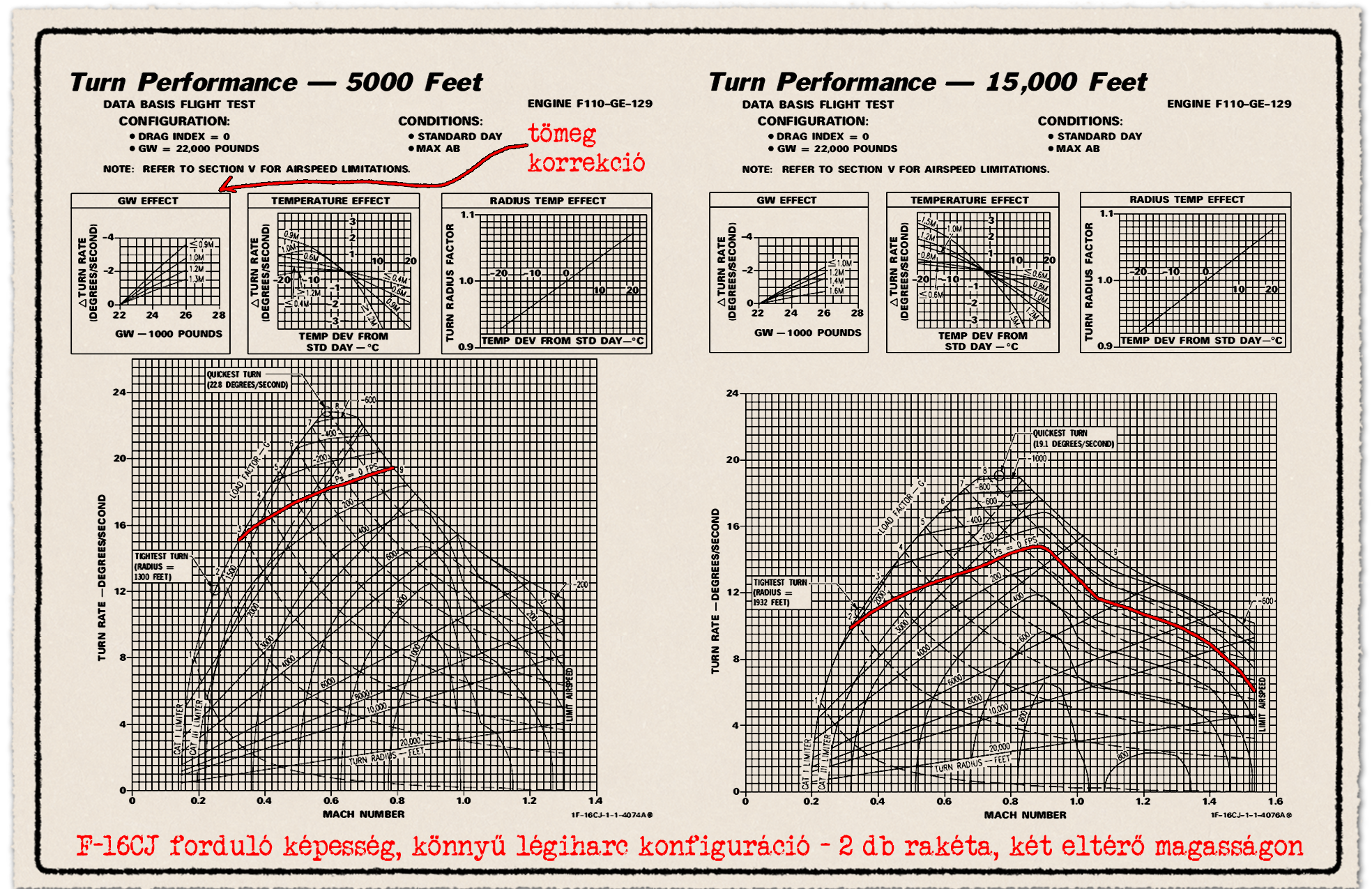
Csak, hogy kontextusba helyezzük a fenti két, ma már igen öreg vadászgépet érdemes csak egy gyors pillantást vetni az F-16C Block 50 vadászgép teljesítményére. Ez az erősebb F110-GE-129 hajtóművel rendelkezik az Block 52 F100-PW-229 hajtóművével szemben. A 0,6-0,9 Mach tartományban az F-4 és F-5 vadászgépek Ps = 0 értéke 12-14 fok/másodperc forduló szögsebesség táján van 5000 láb magasságban, addig ez az F-16-nál 18-19 fok/sec, és majdnem 9G-nél. Drag Index = 0 az a két szárnyvégi AIM-9 vagy AIM-120 rakéta hordozásakor igaz, a 22000 font tömeg nagyjából 1/3 belső üzemanyagot jelent. Ha kb. 1500 fonttal nehezebb lenne az F-16, hogy 50% belső üzemanyag legyen, mint az F-4 és F-5-nél, akkor se lenne más az eredmény. A diagramon leolvasható értékekhez képest kb. 1 fok/másodperccel kisebb forduló szögsebeség adódik ki. Ezt a korrekciót amúgy a nagy diagram feletti kis diagram mutatja.

15 ezer lábnál sem változik az összkép, ahogy már megszoktuk, a növekvő magassággal összenyomódik a diagram. A Ps = 0, tehát a fenntartható forduló szögsebesség mellet az elérhető maximum is csökken, amihez ráadásul nagyobb negatív értékű Ps tartozik. Tehát képes egy nagyon rövid időre a hangsebesség közelében a 18-19 fok/másodperc forduló szögsebessége előállítására az F-16C, de sokkal jobban lassul, mint 5 ezer lábon 22 fok/másodperc értéknél.

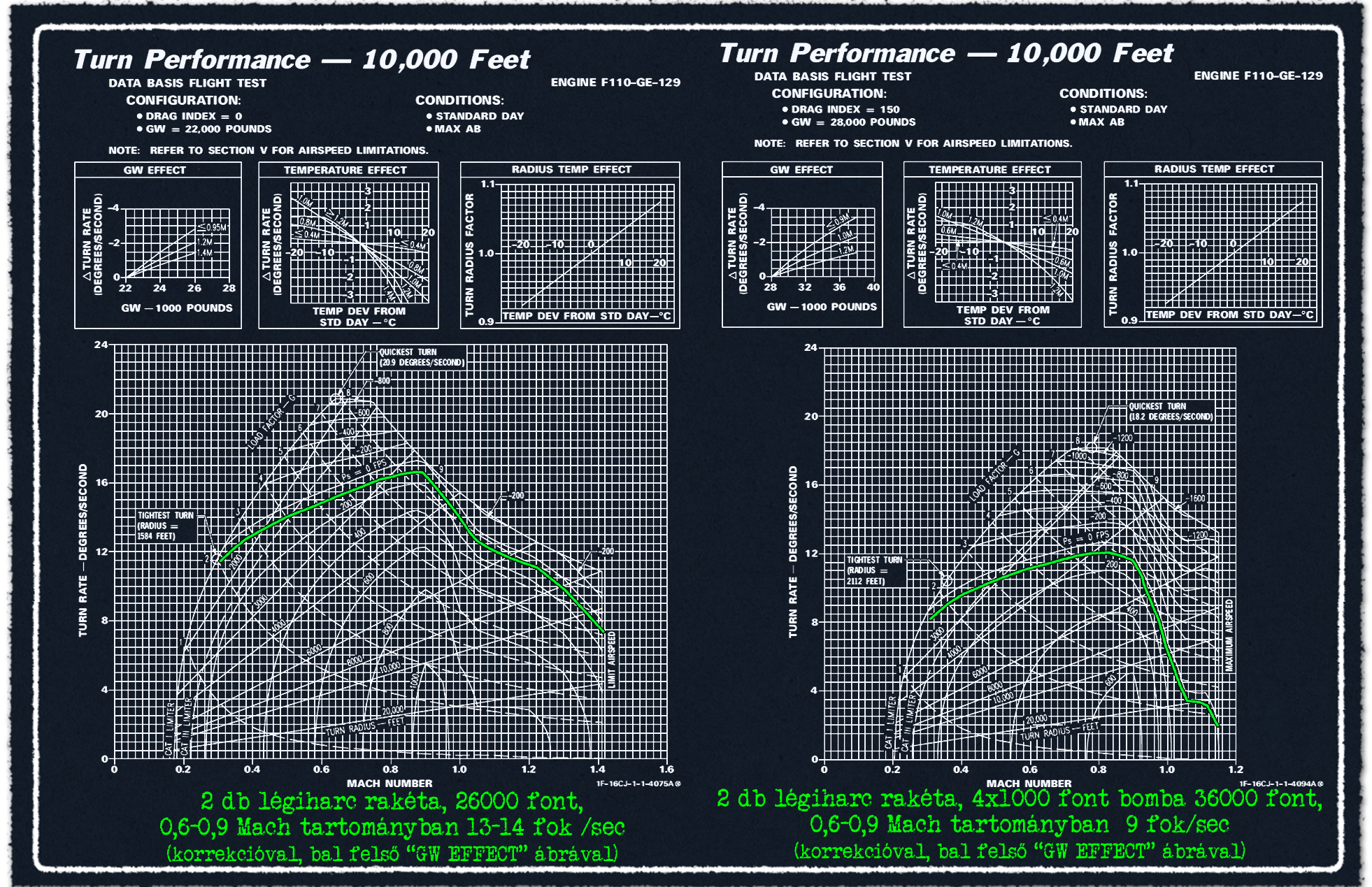
A téma lezárásaként még érdemes rápillantani a csapásmérő konfigurációban jelentkező manőverezőképesség csökkentésre, hogy érezzük szó szerint mindannak a súlyát, amit az anyag első része fejtegetett, hogy mennyire brutálisan hazavágja a teljesítményt a külső függesztmények hordozása. Nagyobb tömeg és légellenállásoknál sajnos csak a 10 és 20 ezer láb magasságon érhető el diagram, lássuk a kisebb magasságon, hogy legalább némi esélye legyen a nehezebb gépnek, hogy a tolóerő azért még viszonylag elfogadható legyen.

A könnyebb F-16C-t két darab légiharc rakétával és 100% belső tüzelőanyaggal vesszük. A nehezebbnél szintén 100% belső üzemanyaggal, de két üres póttartállyal, elektronikai zavarókonténerrel és 4 db 1000 font tömegű csapásmérő fegyverrel. A légiharc konfigurációban repülő gép tömege ekkor kb. 27 ezer font, a csapásmérő konfigurációval repülőé kb. 36 ezer font. A csapásmérő gép légellenállási indexe nagyjából megfelel a diagramon szereplő 150-es értéknek.

A könnyű, kis légellenállású konfigurációban a 0,7-0,9 Mach tartományban a Ps = 0 vonal kb. 16-17 fok/másodperc tartományban van, amiből a szubszonikus sebesség és 26 ezer font tömeg miatt kb. 2,5 fokot kell levonni, tehát valahol a 14-15 fok/másodpercet kapjuk. A csapásmérő konfigurációban a Ps = 0 vonal a 12 fok/másodpercnél van, viszont a 36 ezer font tömeg miatt itt már 3 fokot kell levonni. Azért az így kapott 9, és a 14-15 fok/ másodperc között lehet, hogy a számszaki eltérés nem tűnik nagynak, de a relatív eltérés több, mint 50 (!) százalék.

Ehhez a témához még csak annyit, hogy ha két vadászgép teljesítménye fegyverzet nélkül kb. azonos, akkor nehezebb vadászgép számára a plusz tömeg és fegyverzet hordozása jellemzően kevésbé rontja le a teljesítményt. Ameddig egy F-16 számára 2 tonna csapásmérő fegyverzet és két 370 gallonos póttartály már igen komoly plusz teher és homlok ellenállás növekedést okoz, addig egy kétszer nehezebb F-15E számra 2 tonna fegyverzet és 1 db 600 gallonos póttartály közel sem okoz akkor teljesítmény romlást.

 Hatósugár, légiharc kontra csapásmérés

Amire még érdemes kitérni vadászgépek üzemanyag fogyasztása és hatósugara. A maximális és szubszonikus elfogásnál már néhány érték felvillantásra került, de azok inkább a „mit és miért nem lehet” vonalon mozogtak. Az F-16 lesz az egyik viszonyítási pont, hogy lássuk üzemanyag fogyasztásban mekkora eltérések lehetnek bevetési profiltól és fegyverzettől függően. A cél a távolságra feljogosított átlagfogyasztás megismerése, hiszen azzal lehet könnyen hatósugarat becsülni. Ezeket az adatokat hol táblázatosan, hogy karakterisztika görbék formájában tartalmazzák a vadászgépek üzemeltetési kézikönyvei.

A harcászati kényszerűség, vagyis a bevetési profil miatt a vadászgépek nagyon sokszor nem repülhetnek sem az optimális utazómagasságban sem optimális utazósebességgel. Például a csatornán bemutatott Opera Hadművelet alatt a célponthoz végig terepkövető profillal repültek, de az ahhoz tartozó gazdaságos sebességen. Majd a célpont közelébe érve még mindig terepkövető módon, de maximálgáz teljesítménnyel, ami minden, csak nem a leggazdaságosabb. Hazafelé meg már gazdaságos utazósebességgel és magasságon haladtak. Lássuk hát nagyjából ezen eseteket F-16C Block 50 vadászgéppel, a korábban már használt csapásmérő konfigurációval.

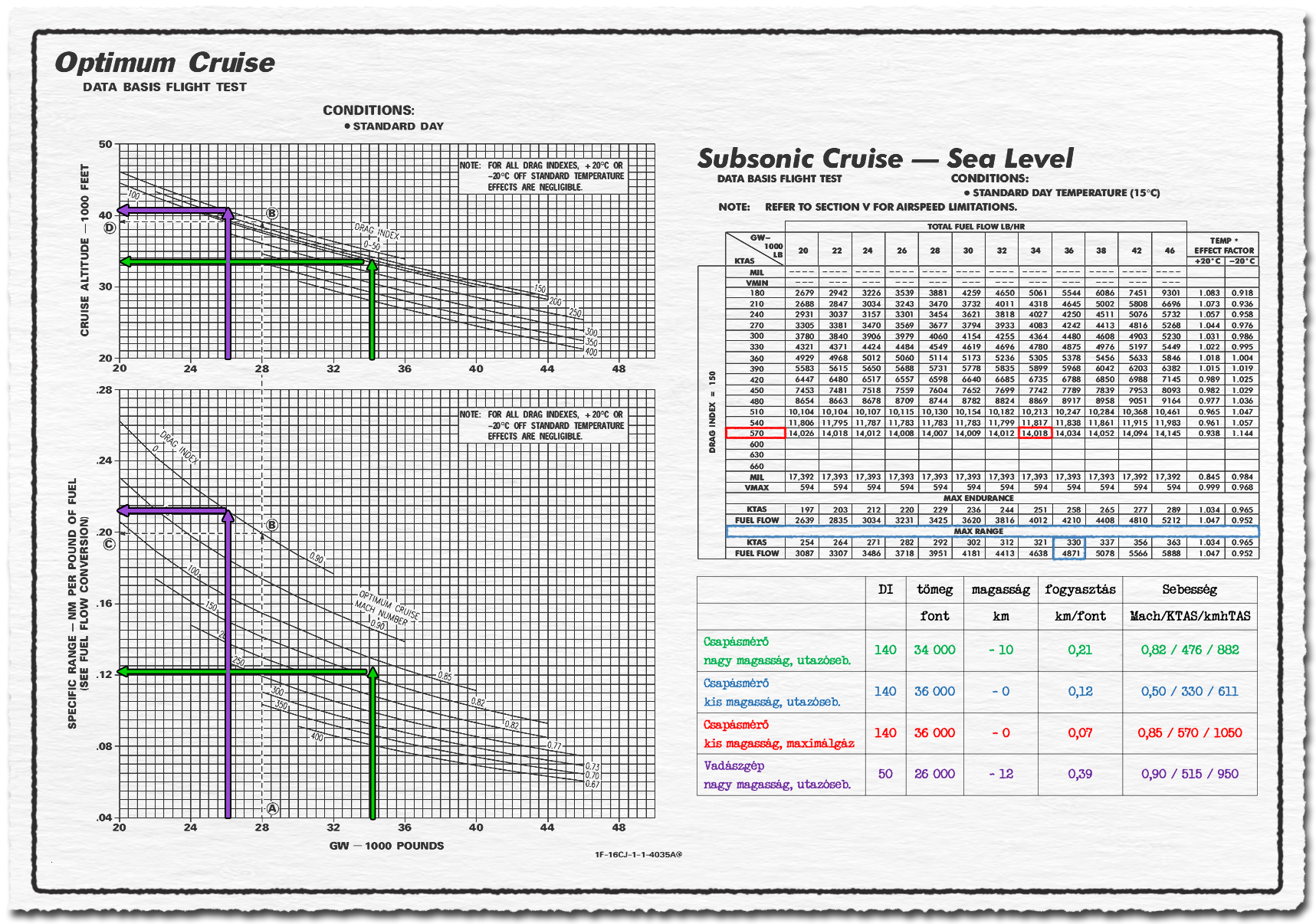
Felszállás és gyorsítás után kb. 38 ezer font tömeg, a légellenállás tényező a DRAG INDEX 140, ezt vehetjük a diagramon leolvasás szerint 150-nek. A gazdaságos utazómagasságra emelkedésre saccoljunk 1000 font üzemanyagot, ami közben már lehet a célpont felé is repülni. Valójában amúgy az emelkedéshez szükséges üzemanyag számítására is léteznek diagramok, csak most az egyszerűsítés kedvéért élek ezzel. 36 ezer font és 140-es DRAG index mellett az optimális utazómagasság 33 000 láb, tehát kb. 10 kilométer magasan van. Az optimális utazósebesség 0,82 Mach, ez 882 km/h. A fajlagos fogyasztás 0,115 tengeri mérföld / 1 font üzemanyag, ez 0,21 km / 1 font kerozin.

Ezzel szemben mi volt a realitás, amikor végig terepkövető repülésben kellett a célpont felé repülni? Az igaz, hogy az emelkedés üzemanyag igényét meg lehet spórolni, de a fogyasztás útvonalrepülés közben számottevően magasabb lesz. Az még hagyján, de még lassabban is kell repülni... Az optimális sebesség tengerszinten csak 611 km/h, ami 0,5 Mach. A táblázat a fogyasztást időre fajlagosítva, 1 órára adja meg. Tehát a megtett távolságot, ami az utazósebességből adódik azt kell a 4871 font/óra fogyasztással. 611 km/h osztva a 4871 font/h fogyasztás értékkel az 0,12 km /font. Tehát a fogyasztás 40%-kal magasabb úgy, hogy 30%-kal lassabban kell repülni az optimális utazómagasságon érvényes utazósebességhez képest.

Harcászatilag nagyon nem mindegy, hogy mennyi ideig és mekkora sebességgel repül az ember ellenséges légtérben. Utánégető használata nélkül is lehet a hangsebesség közelében repülni, de annak komoly ára van. A táblázat szerint 570 csomó, vagyis 1050 km/h sebességnél – ez amúgy 0,85 Mach – az óránkénti üzemanyag fogyasztás nagyjából 14 000 font/óra. Emiatt a távolságra számolt fogyasztás 0,07 km / 1 font üzemanyag. Ez 42%-kal kisebb fajlagos hatótávolság, mint az utazósebességgel számolt érték. Tehát csak nagyon indokolt esetben gyorsítanak fel a gépek, ha a hatósugaruk határán repülnek. Lényegében a célpont közvetlen közelében vagy, ha menekülni szükséges. Aztán hazafelé lehet imádkozni, hogy ne legyen erős szembeszél vagy bármi egyéb váratlan esemény és a tartalék elég legyen...

Mi a helyzet, ha légiharc konfigurációról beszélünk? Hat darab légiharc, rakétával, pilonokkal és 50% belső üzemanyaggal repülő gép tömege kb. 26 ezer font, a DRAG INDEX jó közelítéssel 50. Ezzel az optimális utazómagasság 40 ezer láb, az utazósebesség 0,9 Mach, az üzemanyag fogyasztás 0,21 tengeri mérföld/font, ami 0,39 km / 1 font üzemanyag. Ez 3,25-szerese a tengerszinti csapásmérő, gazdaságos fajlagos hatótávolságnak úgy, hogy 50 (!!) százalékkal gyorsabban repül az F-16. Egészen elképesztő szélsőségek. Ilyen brutális hatása van a hullám- és légellenállának és a repülési magasság együttesének. Ezért van az, hogy az autóskártyás, egyszámjegyes hatósugár egy értelmezhetetlen dolog egy harci gépnél, ha nem írják oda, hogy azt hogyan értelmezik.

Amit még érdemes megvizsgálni, hogy csökkenő tömeg, de azonos légellenállási tényező hogyan befolyásolja az üzemanyag fogyasztást. Mitől csökken a fogyasztás? A vízszintes repüléshez is felhajtóerőt szükséges előállítani. Az előző részben már tisztáztuk, hogy a nagyobb felhajtóerő előállítása nagyobb légellenállással jár. Tehát ahogy csökken egy repülőgép tömege, akkor azonos sebesség mellett egyre kisebb állásszöggel repülés is elég a szüksége felhajtóerő előállításához, tehát kisebb a légellenállás is.

Az ábrán az F-15 vadászgép fajlagos fogyasztás értékei láthatók 30 ezer láb, nagyjából 9 kilométer magasan. Egy három póttartályos, 4+4 légiharc rakétával repülő F-15 DRAG INDEX értéke kb. 40. Az F-15 üres tömege kb. 28 000 font. A belső 11 000 font készlet mellett a három 600 gallonos póttartályban még 12 ezer font üzemanyag betöltése lehetséges. Számoljuk a teljes mennyiség 80%-val, a többi elment az emelkedésre és felszállásra. A tömeghez hozzájön még a 4+4 rakéta tömege, ami kb. 2500 font.

Tehát nagy magasságon a gazdaságos utazósebességet kezdetben nagyjából 52 000 font tömeggel szükséges nézni. Ez kb. 0,095 tengeri mérföld / 1 font üzemanyag, ami 0,8-es értékkel, a légellenállás miatti faktorral kell korrigálni. Ezzel a 0,076 tengeri mérföld / 1 font üzemanyag fogyasztás kapjuk.

Mi a helyzet akkor, ha még a póttartályok a gépen vannak, de már csak a belső üzemanyaggal repül? Akkor kb. 40 ezer font a gép tömege, változatlan DRAG INDEX mellett. 0,105-ös leolvasott értéket 0,82-es faktorral korrigálva a fogyasztás 0,086 tengeri mérföld / 1 font. Ez 13%-kal kisebb érték. Nem egetrengető, de azért ez már számottevő.

Mi történik, ha eldobja mind a három póttartályt az F-15. A tömegüket ezeknek hanyagoljuk el, viszont a DRAG index 40-ről leesik kb. 20-ra. Ezzel 0,105 leolvasott értékhez, ami valójában ennél picit magasabb lenne, már a 0,91-es korrekciós faktor társul. Ezzel további 10%-kal javul a fajlagos fogyasztás.

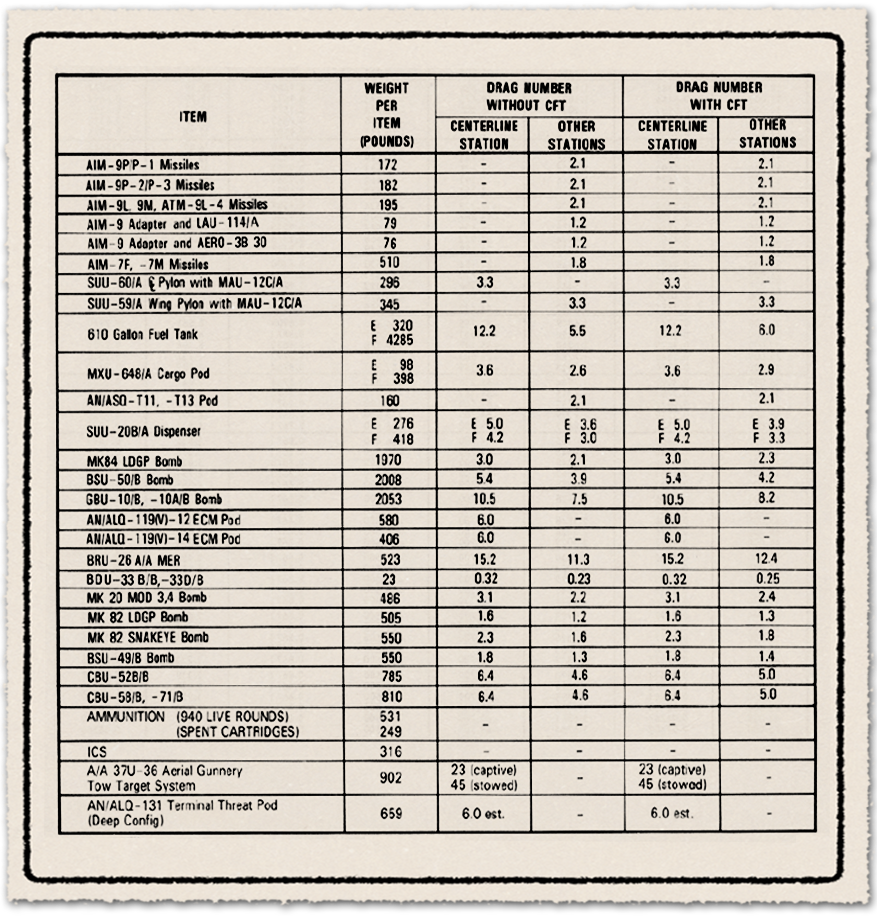
De ez a modell még ott csal lefelé, hogy minél könnyebb a gép, annál magasabbra adódik az optimális utazómagasság. A könnyű és kis légellenállású F-15 optimális utazómagassága nem 30 ezer, hanem 40 ezer láb táján van. Ott a leolvasható fogyasztás 0,125, a korrekció faktor azonos. Tehát a fajlagos hatótávolság a 30 ezer láb és nehéz géphez képest valójában 50%-kal nőtt, és ebből nagyjából fele-fele arányban felelős a tömeg és a légellenállás, ha a kisebb tömeg mellé mindig adottnak vesszük a magasabbra emelkedést.

Ez amúgy azt a sokszor tévesen idézett generális állítást cáfolja, hogy a póttartályokban hordozott üzemanyag mennyiség 70%-a saját légellenállás legyűrésére fordítódik. Az F-15 a belső kapacitását póttartályokkal megduplázva még 50%-kal sem növeli meg a fajlagos fogyasztást. Tehát az arány még extrém módon nehéz és nagy légellenállású gépnél is inkább 50-50%, de ez lehet magasabb is, ez a hordozó gép és a póttartály méretétől is függ. A legenda ugyanis elhallgatja az utazósebességre gyakorolt hatását a tömegnek és légellenállásnak, pedig nagyon fontos tényező az utazósebesség megváltozása is.

 Összefoglalás

Végül összegezzük mindazt, amit láttunk a diagramokon.

• A vadászrepülők légiparádén bemutatott bámulatos irány- és magasság változtató képességei csak fegyvertelenül, kismagasságon, néhány percre repülésre elég üzemanyaggal érhetőek el. Fegyverzettel és a magasság növekedésével ezek még légiharc-konfigurációban is érezhetően romlanak. A hollywoodi és egyéb zs kategóriás filmekben látható dolgokat nagyjából ignorálni lehet. Látványosak, de semmi közük nincs a valósághoz, lényegében teljes mértékben figyelmen kívül hagyják a fizikát.

Nagy magasságban, 9-10 km táján a vadászgépek fenntartható forduló szögsebessége 5-6 fok/sec tartományba zuhan még légiharc konfigurációban maximális utánégetéssel. Csapásmérő fegyverzettel, maximálgáz hajtómű teljesítménnyel lényegében a kereskedelmi utasszállítók teljesítmény tartománya felé konvergálnak. Példaként, egy alaposan megpakolt F-15E fenntartható túlterhelése még a 2G-t sem éri el úgy, hogy hangsebeség közelében, 0,8 Mach táján repül, nagyjából 3/fok sec forduló szögsebességgel.

• Légiharc fegyverzettel a külső függesztéssel a vadászgépek reálisan kihasználható csúcssebessége 1,3-1,4 Mach táján van, csak éppen a szubszonikus hatótávolság töredékével még akkor is, ha végig nagy magasságban történik a gyorsítás és a sebesség tartása. Ez alól lényegében csak az MiG-25 és MiG-31 és esetleg az F-22 Raptor kivétel, de ennek paraméterei nem publikusak.
• A vadászrepülőgépek csúcssebessége és elérhető maximális gyorsulása teljesen más sebesség és magasság tartományban van és ezek között nincs is feltétlen közvetlen kapcsolat.
• Minden vadászgép, ami külső függesztéssel hordoz fegyverzetet és póttartályt, annak csapásmérő konfigurációban, valós harcászati helyzetben értelmezett csúcssebessége hangsebesség alatti. Pont. Minden más állítás csak bugyuta kijelentés, amin legfeljebb csak mosolyogni lehet.

Egy vadászgép elvi szinten képes lenne éppen csak átlépni a hangsebességet 8-10 kilométer magasan korlátozott mennyiségű csapásmérő fegyverzettel, póttartály nélkül, de az olyan sokáig tart és akkora üzemanyag igénye van, hogy teljesen értelmetlen lenne azt bármilyen harc helyzetben megpróbálni is. Nincs olyan elképzelhető harcászati helyzet, ahol ennek érelme lenne. Póttartályokkal és csapásmérő fegyverzettel a legtöbb vadászgép fizikailag sem képes átlépni a hangsebességet. A hullámellenállás olyan eszementen nagy, hogy maximális utánégetéssel sem lehetséges az vízszintes repülésben.

• A vadászgépek hatósugara a bevetési profiltól függően akár három-tízszeres eltérést is mutathatnak. Ez adódhat a nagysebességű elfogás vagy a hordozott függesztmények és a bevetési profiltól, hogy kis- vagy nagy magasságban zajlik-e a repülés döntő része. Az egyetlen számmal jellemzett hatótávolság hatósugár egy teljesen használhatatlan érték.
• A belső fegyvertérrel rendelkező, újgenerációs vadászgépek teljesítménye számottevő mértékben meghaladhatják a hagyományos vadászgépekét, erről bővebben az extra tartaloman esik szó.

 Közreműködők

• Molnár Balázs                                Grafika, animáció, szöveg
• Hpasp                                             Technikai lektor
• Cifka”Cifu” Miklós                           Technikai lektor
• Farkas Gábor                                  Technikai lektor

 A Patreon és Donably felületek elérhetősége az extra tartalomhoz és támogatásához.

https://www.patreon.com/militavia

https://www.donably.com/militavia-katonai-repules-legvedelem